Математичні операції в СЗК
Розглянемо правила виконання операцій додавання і множення в СЗК при умові, що обидва числа і результат операції знаходяться в діапазоні Нехай операнди А і В представлені відповідно залишками Результат операцій додавання і множення
і при цьому мають місце співвідношення:
Припускається, що
При цьому в якості цифри результату береться відповідно
Отже, можна записати для додавання
для
Для множення
Приклад: нехай основою системи є Діапазон представлення чисел за допомогою вибраних модулів визначається, як
Приклад. Додати числа А=17 і В=63. Переведемо числа А і В в систему залишкових класів по заданих модулях
В відповідності з (2.10) отримаємо
Легко перевірити, що число
Приклад. Помножити число А=17 на число В=6. В СЗК числа А і В будуть представлені як
В відповідності з (11) отримаємо Легко перевірити, що число Правила виконання операції віднімання в СЗК в випадку, якщо два числа і результат операції знаходяться в діапазоні Нехай операнди А і В представлені відповідними залишками Результат операції віднімання А-В представлений відповідними залишками Тобто
і при цьому виконуються умови:
Аналогічно з (10) отримаємо вираз для віднімання
Операція віднімання в тих випадках, коли її результат додатній, виконується відніманням відповідних цифр розрядів, при цьому завжди в результаті приводиться найменший додатній залишок, так як це випливає із визначення СЗК. Якщо різниця цифр від’ємна, то береться її доповнення до відповідного модуля. Тобто
Приклад. Виконати віднімання двох чисел в СЗК. С=А-В.
В результаті послідовного застосування прямого та зворотного перетворень для цілочисельної форми СЗК отримаємо вихідне число в позиційній системі числення. Представлення даних в системі залишкових класів дає змогу здійснювати розпаралелювання обробки інформації без значного ускладнення обчислювальних засобів. Використання СЗК спрощує побудову систем збору інформації, а також дозволяє вирішувати клас задач, що є невизначеними в позиційних системах числення. Особливістю СЗК залишається простота реалізації прямого та зворотного перетворень.
Контрольні запитання 1. Назвіть переваги та недоліки СЗК? 2. Переведіть задані числа з десяткової СЧ в СЗК. 3. Переведіть задані числа з СЗК в десяткову СЧ. 4. Виконайте арифметичні операції в СЗК.
|

 .
. і
і 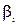 по модулю
по модулю 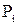 при
при 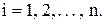
 і
і 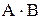 представлені відповідними залишками
представлені відповідними залишками 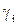 і
і  по тих же модулях
по тих же модулях 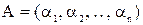 ,
,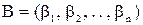 ,
,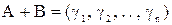 ,
,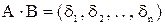 ,
, ,
, 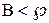 ,
, 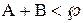 ,
, 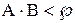 .
.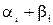 по модулю
по модулю 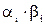 також по модулю
також по модулю 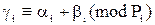 ,
, .
.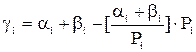 (10)
(10)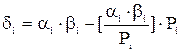 . (11)
. (11)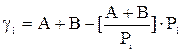 ,
,
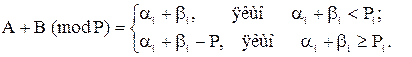
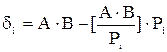 .
.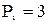 ,
, 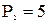 ,
, 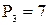 .
. =105.
=105.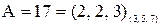 ,
, .
. .
.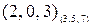 в десятковій системі числення є 80 і дорівнює сумі операндів.
в десятковій системі числення є 80 і дорівнює сумі операндів. .
. .
. в СЗК дорівнює десятковому числу 102 в десятковій системі числення і рівне добутку операндів.
в СЗК дорівнює десятковому числу 102 в десятковій системі числення і рівне добутку операндів.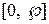 .
.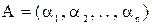 ,
,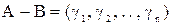 ,
,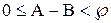 .
. ,
,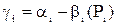 ,
, 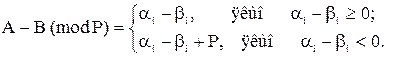
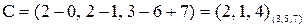 .
.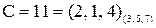 .
.


