При использовании этого метода за период жизни проекта средняя чистая прибыль сопоставляется со средними инвестициями (затратами основных и оборотных средств) в проект.
Метод прост для понимания и включает несложные вычисления, благодаря чему может быть использован для быстрой отбраковки проектов. Однако существенным недостатком является то, что игнорируются неденежный (скрытый) характер некоторых видов затрат (например, амортизационных отчислений) и связанная с этим налоговая экономия; доходы от ликвидации старых активов, заменяемых новыми; возможности реинвестирования получаемых доходов и времення стоимость денег. Метод не дает возможности судить о предпочтительности одного из проектов, имеющих одинаковую норму прибыли, но разные размеры средних инвестиций:
где NI – чистая прибыль по проекту; IC – инвестируемый капитал. Чистая приведенная стоимость (Net Present Value – NPV) NPV характеризуют превышение суммарных денежных поступлений над суммарными затратами соответственно без учета и с учетом неравноценности эффектов (результатов и затрат), относящихся к различным моментам времени. Если чистая текущая стоимость проекта NPV положительна, то проект может считаться приемлемым. В случае оценки финансовых активов метод работает безупречно. С точки же зрения полноты и его применимости в расчетах для реальных инвестиционных проектов он нуждается в некотором усовершенствовании. Учитывая первые два момента (третий момент на формуле не отражается, но должен быть учтен в расчетах), формулу расчета чистого приведенного эффекта для реального инвестиционного проекта можно записать в следующем виде:
где
r – норма (ставка) дисконтирования; n – число шагов за период реализации проекта. Общее правило для NРV: если NPV > 0, проект принимается, в противном случае его следует отклонить. Метод NPV не позволяет судить о пороге рентабельности и запасе финансовой прочности проекта. Метод неточно определяет влияние изменений стоимости недвижимости и сырья на чистую приведенную стоимость проекта. Его использование осложняется трудностью прогнозирования ставки дисконтирования (средневзвешенной стоимости капитала) и (или) ставки банковского процента. Внутренняя норма доходности, или внутренний коэффициент Если вернуться к описанным выше уравнениям NPV, то IRR – это то значение r в этих уравнениях, при котором NPV будет равна нулю:
где
n – срок реализации инвестиционного проекта, годы. Модифицированный показатель оценки внутренней нормы Этот показатель используется для устранения недостатков метода IRR, вычисляется на основе следующего уравнения:
где n – общая продолжительность проекта; t – текущий период реализации проекта;
r – ставка дисконтирования (стоимость привлеченного капитала, требуемой нормы рентабельности инвестиций, Capital Cost (CC) или WACC), в долях единицы; d – стоимость капитала, по которой реинвестируются денежные притоки, в долях единицы. Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения по инвестициям, уровень рентабельности которых не ниже стоимости капитала (CC). Именно с ним сравнивается показатель MIRR, рассчитанный для конкретного проекта, при этом связь между ними такова: если MIRR > CC, то проект следует принять; MIRR < CC, то проект следует отвергнуть; MIRR = CC, то проект ни прибыльный, ни убыточный. Рентабельность инвестиций (индекс рентабельности) PI Этот показатель позволяет определить, в какой мере возрастает прибыльность проекта (богатство инвестора) в расчете на 1 руб. инвестиций. Расчет показателя рентабельности производится по формуле
где
r – ставка дисконтирования. Очевидно, что если NPV положительна, то и PI будет больше единицы и соответственно – наоборот. Таким образом, если расчет дает нам PI больше единицы, то такие инвестиционные вложения целесообразны.
|


 ,
, ,
,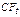 – поступления от реализации инвестиционного проекта в году t;
– поступления от реализации инвестиционного проекта в году t; – инвестиционные вложения в разные периоды t реализации инвестиционного проекта;
– инвестиционные вложения в разные периоды t реализации инвестиционного проекта; – остаточная стоимость активов по окончании периода реализации проекта;
– остаточная стоимость активов по окончании периода реализации проекта; ,
, – поток денежных средств в течение n лет;
– поток денежных средств в течение n лет; – исходная величина инвестиционных вложений;
– исходная величина инвестиционных вложений; =, или
=, или  ,
, – отток денежных средств в t -м периоде;
– отток денежных средств в t -м периоде; – приток денежных средств в t -м периоде;
– приток денежных средств в t -м периоде;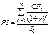 ,
,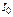 – первоначальные инвестиционные вложения;
– первоначальные инвестиционные вложения; – денежные поступления в году t;
– денежные поступления в году t;


