Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами).
Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках  и
и  :
:
 (4)
(4)
где 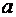 и
и 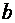 - полуоси эллипса, с – полуфокусное расстояние. Коэффициенты
- полуоси эллипса, с – полуфокусное расстояние. Коэффициенты  эллипса связаны соотношением
эллипса связаны соотношением 

Рис. 3
Если центр эллипса находится в точке  , то уравнение эллипса имеет вид:
, то уравнение эллипса имеет вид:

3. Гипербола
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Уравнение гиперболы с центром в начале координат и с фокусами в точках  и
и  имеет вид:
имеет вид:
 (6)
(6)
где 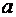 - действительная полуось,
- действительная полуось,
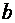 - мнимая полуось
- мнимая полуось
Коэффициенты  и
и  гиперболы связаны соотношением
гиперболы связаны соотношением  .
.
Прямые 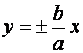 - асимптоты гиперболы.
- асимптоты гиперболы. 
Если центр гиперболы находится в точке  , то уравнение имеет вид:
, то уравнение имеет вид: 
4. Парабола
Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.
Уравнение параболы с вершиной в начале координат имеет вид:
 , где
, где  - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты  .
.

Если вершина параболы находится в точке  , то уравнение имеет вид:
, то уравнение имеет вид:

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов  отличен от нуля.
отличен от нуля.
6. Определение 1.1. Матрицей называется прямоугольная таблица чисел.
Обозначения: А — матрица, - элемент матрицы, номер строки, в которой стоит данный элемент, номер соответствующего столбца; m — число строк матрицы, n — число ее столбцов.
Определение 1.2. Числа m и n называются размерностями матрицы.
Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило
треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так: образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали.
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a`ij = aji Основные свойства определителей.
Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).
Свойство 1. Определитель не изменяется при транспонировании.
Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число.
Свойство 3. Определитель, имеющий нулевую строку, равен 0.
Доказательство этого свойства следует из свойства 2 при k = 0.
Свойство 4. Определитель, имеющий две равные строки, равен 0.
Свойство 5. Определитель, две строки которого пропорциональны, равен 0.
Доказательство следует из свойств 2 и 4.
Свойство 6. При перестановке двух строк определителя он умножается на —1.
Свойство 7.Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.
Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
Доказательство следует из свойств 7 и 5.
Разложение определителя по строке.
Определение1. 7. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.
Обозначение: выбранный элемент определителя, его минор.
Определение1. 8. Алгебраическим дополнением элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
Рассмотрим еще один способ вычисления определителей третьего порядка — так называемое разложение по строке или столбцу. Для этого докажем следующую теорему: Теорема 1.1. Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е. где i=1,2,3.
Доказательство.
Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат.
Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.
Пример. Вычислим определитель с помощью разложения по первому столбцу. Заметим, что при этом искать не требуется, так как следовательно, и Найдем и Следовательно,
7. Системы линейных уравнений
Обозначим через любое из множеств или.
Системой линейных уравнений (л.у.) над называется совокупность (набор) из нескольких уравнений от одного и того же набора переменных (неизвестных).
здесь числа и — из; они называются коэффициентами системы. Первый индекс у коэффициента отвечает за номер уравнения, а второй — за номер переменной. Относительно числа уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных. Если то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной -- в противном случае, то есть в случае, когда решений у системы нет.
Однородные системы линейных уравнений
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
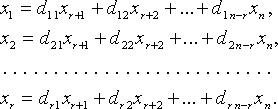 Тогда n - r линейно независимыми вектор-решениями будут:
Тогда n - r линейно независимыми вектор-решениями будут:

а любое другое решение является их линейной комбинацией. Вектор-решения  образуют нормированную фундаментальную систему.
образуют нормированную фундаментальную систему.
В линейном пространстве  множество решений однородной системы линейных уравнений образует подпространство размерности n - r;
множество решений однородной системы линейных уравнений образует подпространство размерности n - r;  - базис этого подпространства.
- базис этого подпространства.
Правило Крамера
Рассмотрим частный случай системы линеных уравнений (15.1), когда  , то есть когда число уравнений совпадает с числом неизвестных. Именно такие системы при
, то есть когда число уравнений совпадает с числом неизвестных. Именно такие системы при  или
или 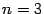 рассматриваются в школе.
рассматриваются в школе.
Если число уравнений равно числу неизвестных, то матрица 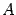 исходной системы -- квадратная,
исходной системы -- квадратная,
порядка  ,
,  и
и  -- столбцы высоты
-- столбцы высоты  . Предположим, что
. Предположим, что  . Тогда по теореме 14.1 существует обратная матрица. Умножив слева обе части равенства (15.2) на
. Тогда по теореме 14.1 существует обратная матрица. Умножив слева обе части равенства (15.2) на  , получим
, получим 
Таким образом, система уравнений (15.1) имеет единственное решение и оно в матричной форме может быть записано в виде
Это так называемый
матричный способ решения системы линейных уравнений.
Введем следующие обозначения. Пусть

,

-- определитель матрицы, полученной из матрицы
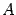
заменой столбца с номером
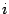
на столбец

свободных членов,
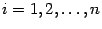
:

Теорема 15.1 (Правило Крамера) Если в системе  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  , то система имеет решение и притом единственное. Это решение задается формулами
, то система имеет решение и притом единственное. Это решение задается формулами

Доказательство. По теореме 14.1 обратная матрица находится по формуле

где  -- алгебраические дополнения. Тогда из (15.3) следует, что
-- алгебраические дополнения. Тогда из (15.3) следует, что

Заметим, что по формуле (14.13) разложение определителя  по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя
по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя  по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому
по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому  , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.
Пример 15.1 Решите систему уравнений 
Решение. Выписываем матрицу системы  и столбец свободных членов
и столбец свободных членов  .
.
Находим определитель системы:  . Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:
. Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

Итак,

Ответ:  .
.
8. Свойства функции
Функция - это одно из важнейших математических понятий. Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу - Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.
9. Предел функции.
Определения и примеры.
Пусть EМ R и a – предельная точка множества E.
Определение 1. Будем говорить, что a –предельная точка для множества E, если любая окрестность точки a содержит бесконечное подмножество множества E.Пусть f:E ® R. Приведем несколько формулировок определения предела функции. Для разных оценок бывает удобна то одна, то другая.
Определение 2 (предел функции по Коши). Число A О R называется пределом функции f(x) в точке a или при x® a и это обозначается следующим образом lim x ® af (x) = A, если" e > 0 $ d(e)>0: " x: 0 <|x-a|< d, Ю |f (x) -A|< e
Пример 1. Доказать, что limx® 1(2x+3) = 5.
Запишем определение предела для данного примера" e >0 $ d (e)>0 " x удовлетворяющих условию: 0 <|x- 1 |<;dдолжно быть выполнено неравенство | 2 x+ 3-5 |<;e или 2 |x- 1 |<;e.Отсюда следует, что неравенство 2|x-1|<2d<e выполнится, если dЈe/2. Если e = 0,1, то d = 0,05, при e = 0,01, d = 0,005 и т.д. Таким образом, решение задачи состоит в нахождении d, зависящего от e.
Определение 3. Проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.
Обозначается проколотая окрестность символом  .
.
Определение 4 (предел функции на "языке окрестностей"). Число A О R называется пределом функции f(x) в точке a или при x® a, если для любой окрестности U (A) числа A существует проколотая окрестность  точки a такая, что f (
точки a такая, что f ( ) М U (A).
) М U (A).
Приведем еще одно эквивалентное определение предела на "языке последовательностей".
Определение 5 (предел функции по Гейне). A=limx ® af(x)
означает, что" xn ® a при n ® Ґ; xn № a, f (xn) ® A при n ® Ґ Пример 2. Покажем, что не существует предела f(x) = sin(1/x) при x® 0. Для этого используем определение предела на языке последовательностей. Выберем две последовательности xn1 = 1/p n, xn2 = 1/(p/2+2p n), которые обе сходятся к нулю при n®Ґ. Тогда sin xn1 = sin p n=0, sin xn2 = sin (p/2+2p n) = 1, Таким образом, f(xn1) и f(xn2) сходятся к разным числам, поэтому определение предела на "языке последовательностей" не выполняется.
Пример 3. Рассмотрим функцию Дирихле
| f (x) =
| | м 1, если x О Q
| | н
| | о 0, если x О R\ Q
| |
, где
Q – множество рациональных чисел, соответственно множество
R\ Q – множество иррациональных чисел. Данная функция не имеет предела ни в одной точке
a действительной прямой. Действительно, если выбрать последовательность рациональных чисел, сходящихся к
a, то соответствующая последовательность значений функции сходится к единице. Если выбрать последовательность иррациональных значений, то значения функции сходятся к нулю. Следовательно, на основании определения предела по Гейне данная функция не имеет предела.
Рассмотрим геометрический смысл предела функции в точке. Неравенство |f(x)-A|<e равносильно двойному A-e<f(x)<A+e. Число A есть предел функции f(x) при x®a, если для любого e >0 найдется такая d -окрестность точки a, что для всех x№ a из этой окрестности соответствующие значения функции f(x) будут заключены в полосе A-e<f(x)<A+e (см. рис. 14).

Рассмотрим понятие предела функции в бесконечности.
Определение 6 (предел функции в бесконечности).
lim x ® Ґ f (x) = A, если " e > 0 $ B (e) >0: " x таких, что |x| > B, выполняется |f (x) -A| < e
Определение 7. lim x ® af (x) = Ґ, если " A>;0 $ d(A) > 0: " x 0 <|x-a|< d, |f (x) | >A lim x ® Ґ f (x) = Ґ, если " A>;0 $ B (A)>0: " x |x|>B, |f (x) |>A
Аналогично формулируются определения при x® ±Ґ, а также определения, когда A = ±Ґ. Замечание. Изученное понятие предела последовательности можно рассматривать как частный случай предела функции при x® +Ґ.
Замечание. Если при стремлении x к a переменная x принимает лишь значения, меньшие a или большие a и при этом f(x) стремится к A, то говорят, что существуют односторонние пределы функции, то есть limx® a-0f(x) = A – предел слева или limx® a+0f(x) = A – предел справа. Очевидно, что если limx® a-0f(x) = limx® a+0f(x) = A, то limx® a = A. Верно и обратное утверждение.
Свойства предела функции.
Теорема 1 (свойства предела функции).
Если $ lim x ® af(x) = A, то найдется окрестность точки a  такая, что в этой окрестности функция f (x) будет ограничена.
такая, что в этой окрестности функция f (x) будет ограничена.
- Если f (x) есть постоянная A в некоторой окрестности точки a, то lim x ® af (x) = A
- Если lim x ® af (x) = A 1 и lim x ® af (x) = A 2, то A 1 = A 2
Утверждения данной теоремы вытекают из определения предела функции.
Теорема 2 (арифметические операции над пределами).
Если lim
x ®
af (
x)
= A,lim
x ®
ag (
x)
= B, то
- lim x ® a[f(x) ± g(x)]=A ± B,
- lim x ® af (x) g (x) = AB
- lim x ® af (x) /g (x) = A/B, B № 0
Эта теорема непосредственно следует из соответствующей теоремы о пределах последовательностей.
Теорема 3 (предел и неравенства).
Пусть f:E ®
R, g:E ®
R, h:E ®
R
- Если lim x ® af (x) = A, lim x ® ag (x) = B и A<B, то $
 : " x О
: " x О  f (x) <g (x).
f (x) <g (x). - Если для " x О E f (x) Ј g (x) Ј h (x) и существует lim x ® af (x) = lim x ® ah (x) = A. то существует lim x ® ag (x) = A

Разделив эти неравенства на (1/2) x, получим требуемый результат.
- Из выше полученного результата следует, что
| sin
x| Ј
|x| "
x О
R.
- Из 2) по теореме о предельном переходе в неравенствах вытекает, что
lim
x ® 0sin
x = 0.
- Теперь покажем, что
lim
x ® 0(sin
x)
/x = 1.
Cчитая, что |x|<p/2, в силу полученного в 1) неравенства имеем
1-sin2 x<;sin x/x<;1.
Но limx® 0(1-sin 2x) = 1, значит, по теореме о предельном переходе в неравенствах следует, что
lim x ® 0(sin x) /x = 1.
Следствие 1.
lim x ® 0(tgx) /x = 1
lim x ® 0(arcsin x) /x = 1
lim x ® 0 (arctgx) /x = 1
Бесконечно малые и бесконечно большие функции.
Определение 8 (бесконечно малая функция). Функция называется бесконечно малой в точке a или при x ® a, еслиlim x ® af (x) = 0
Заметим, что если функция f(x) имеет предел в точке a, равный A, то функция a(x) = f(x)-A является бесконечно малой в точке a. То есть, если функция f(x) имеет предел A в точке a, то f(x) = A+a, где limx® aa (x) = 0.
Отметим некоторые свойства бесконечно малых функций.
Теорема 4 (свойства бесконечно малых функций).
- Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
- Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.
- Произведение конечного числа бесконечно малых является бесконечно малой.
Доказательство. Докажем для примера первое утверждение теоремы для двух бесконечно малых.
Из того, что существует limx® aa(x) = 0, следует, что " e>0 $ d1(e)>0 такое, что " x: 0<|x-a|<d1 выполняется неравенство
|a(x)|< e/2. Аналогично, из существования предела limx® a b(x) = 0, следует " e>0 $ d2(e)>0 такое, что " x: 0<|x-a|<d2
выполняется неравенство |b(x)|< e/2. Тогда " x: 0<|x-a|<d = min{d1,d2} выполнятся оба неравенства одновременно, то есть
| a(x)+b(x) | Ј | a(x) |+| b(x) |<;e.
Определение 9 (бесконечно большая функция). Функция называется бесконечно большой при x ® a или в точке a, если для любого положительного числа e найдется такое положительное d(e), что для всех x№ a и удовлетворяющих условию |x-a|<d будет выполнено неравенство |f(x)|>e.
Аналогично можно дать определение бесконечно большой при x® Ґ. Приведем его в символической записи:
lim x ® Ґ f (x) = Ґ Ы " e>0 $ d(e)>0 " x:|x|>;d |f (x) |>;e.
Предложение 1. a(x) бесконечно малая функция при x ® a Ы 1 / a(x) — бесконечно большая при x ® a
Пример 11. y = x2 – бесконечно малая функция при x ® 0, а y = 1/x2 – бесконечно большая при x ® 0.
Критерий Коши о существовании предела функции.
Определение 10 (условие Коши). Будем говорить, что функция f(x) удовлетворяет в точке a условию Коши, если для любого положительного числа eнайдется положительное d(e), что для любых x1,x2, удовлетворяющих условию
0 <|x 1 -a|<;d, 0 <|x 2 -a|<;d,
справедливо неравенство
|f (x 1 -f (x 2) |<;e.
Теорема 5 (Критерий Коши).. Для того, чтобы существовал предел функции f (x) в точке a ( lim x ® af (x) = A) необходимо и достаточно, чтобы f(x) удовлетворяла в точке a условию Коши.
Аналогично формулируется условие Коши и доказывается критерий Коши и для случаев правого(левого) пределов в точке a, предела при x® Ґ(±Ґ).
 ,
,  -- определитель матрицы, полученной из матрицы
-- определитель матрицы, полученной из матрицы 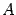 заменой столбца с номером
заменой столбца с номером 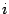 на столбец
на столбец  свободных членов,
свободных членов, 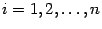 :
:


 и
и  :
: (4)
(4)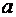 и
и 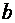 - полуоси эллипса, с – полуфокусное расстояние. Коэффициенты
- полуоси эллипса, с – полуфокусное расстояние. Коэффициенты  эллипса связаны соотношением
эллипса связаны соотношением 

 , то уравнение эллипса имеет вид:
, то уравнение эллипса имеет вид:
 (6)
(6) и
и  гиперболы связаны соотношением
гиперболы связаны соотношением  .
.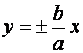 - асимптоты гиперболы.
- асимптоты гиперболы. 

 , где
, где  - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты  .
.


 отличен от нуля.
отличен от нуля.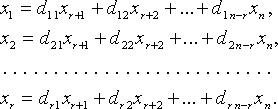 Тогда n - r линейно независимыми вектор-решениями будут:
Тогда n - r линейно независимыми вектор-решениями будут:
 образуют нормированную фундаментальную систему.
образуют нормированную фундаментальную систему. множество решений однородной системы линейных уравнений образует подпространство размерности n - r;
множество решений однородной системы линейных уравнений образует подпространство размерности n - r;  , то есть когда число уравнений совпадает с числом неизвестных. Именно такие системы при
, то есть когда число уравнений совпадает с числом неизвестных. Именно такие системы при  или
или 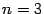 рассматриваются в школе.
рассматриваются в школе. ,
,  и
и  . Тогда по теореме 14.1 существует обратная матрица. Умножив слева обе части равенства (15.2) на
. Тогда по теореме 14.1 существует обратная матрица. Умножив слева обе части равенства (15.2) на  , получим
, получим 


 , то система имеет решение и притом единственное. Это решение задается формулами
, то система имеет решение и притом единственное. Это решение задается формулами

 -- алгебраические дополнения. Тогда из (15.3) следует, что
-- алгебраические дополнения. Тогда из (15.3) следует, что
 по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя
по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя  по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому
по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому  , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.
 и столбец свободных членов
и столбец свободных членов  .
. . Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:
. Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

 .
. .
. 



