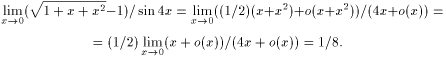Сравнение функций.

Определение 15 (символ О). Если для функций f(x), g(x) существуют постоянные c>0, d>0, такие, что |f(x)|Ј c |g(x)| при |x-a|<d, x№ a, то говорят, что f является ограниченной по сравнению с функцией g в окрестности точки a и пишут, что f(x) = O(g(x)) при x® a.

Данное определение переносится и на случай, когда x® Ґ, x® ±Ґ.

Пример 12.

1. Так как |1/x²| Ј |1/x| при |x| і 1, то 1/x² = O(1/x) при x ® Ґ;
2. 1/x = O(1/x²) при x® 0 так как |1/x|Ј 1/x² при |x|Ј 1.

Запись f=O(1) при x® a означает, что функция f(x) ограничена в некоторой окрестности точки a.

Определение 16 (функции одного порядка). Если f=O (g) и g=O (f) при x ® a Ю f и g — одного порядка при x® a.

Пример 13. Функции f (x) = x (2+sin 1 /x) g (x) = x x ® 0 являются бесконечно малыми одного порядка при x® a, так как

f/g = (x (2+sin 1 /x)) /x = 2+sin 1 /x = | 2+sin 1 /x| Ј 3 Ю f=O (g), g/f = 1 /| 2+sin 1 /x| Ј 1 Ю g=O (f).

Определение 17 (эквивалентные функции). Функции f (x) и g (x) называются эквивалентными при x ® a, если $ f(x): f (x) = f (x) g (x), где lim_{x® a}f (x) = 1.

Иначе говоря функции эквивалентны при x ® a, если предел их отношения при x ® a равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами:

sin x ~ x, x ® 0

(1)

tg x ~ x, x ® 0, arcsin x ~ x, x ® 0, arctg x~ x, x ® 0

e^x- 1 ~ x, x ® 0

ln (1 +x) ~ x, x ® 0

(2)

 

m- 1 ~ mx, x ® 0

(3)

Следующая теорема удобна для применения на практике при вычислении пределов.

Теорема 7. Пусть f(x)~ f 1 (x), g(x)~ g 1 (x) при x ® a Тогда если существует предел

lim _x ® af 1(x) /g 1(x),

то существует

lim _x ® af (x) /g (x),

причем

lim _x ® af 1(x) /g 1(x) = lim _x ® af (x) /g (x).

Пример 14. Найти предел

lim _x ® 0(ln cos x) / sin x 2

Решение. Для решения воспользуемся асимптотическими равенствами (1), (2)

lim _x ® 0(ln cos x) / sin x 2 = lim _x ® 0 (ln(1-2sin² x/ 2)) /x 2 =

= lim _x ® 0(-2sin² x/ 2) /x 2 = -2lim _x ® 0(x 2 / 4) /x 2 = -1 / 2.

Определение 18 (символ о). Говорят, что функция f является бесконечно малой по сравнению с g при x ® a, и пишут f=o(g), x® a, если выполнено соотношение f(x) = a(x)g(x), где lim_{x® a} a(x) = 0. Иначеговоря lim_{x® a} f(x)/g(x) = lim_{x® a} a(x) = 0.

Пример 15.

1. x 2 = o (x) при x ® 0, так как lim _x ® 0 x 2 /x = lim _x ® 0 x = 0;
2. 1 /x 2 = o (1 /x) при x ® + Ґ так как lim _x ® Ґ x/x 2 = lim _x ® Ґ1 /x = 0

Справедлива теорема.

Теорема 8. Для того, чтобы функции f(x), g(x) были эквивалентными при x ® a необходимо и достаточно, чтобы при x ® a выполнялось хотя бы одно из условий

f (x) = g (x) +o (g (x))

или

g (x) = f (x) +o (f (x)).

Заметим, что функции g(x) в первом условии и соответственно функция f(x) во втором называются главной частью функции f (x) (g (x) ).

Пример 16.

1. Функция x – главная часть функции sin x при x® 0, так как sin x = x+o(x) при x® 0;
2. Если P_n(x) = a_nxⁿ+...+a₁x+a₀, a_n№ 0, то функция a_nxⁿ является главной частью P_n(x) при x® Ґ, так как P_n(x) = a_nxⁿ+o(xⁿ) при x® Ґ.

Метод выделения главной части бесконечно малых применяется к вычислению пределов.

Пример 17. Найти предел

Решение. Используя асимптотическое равенство (3) и асимптотическое равенство (1), а также учитывая, что x 2 = o (x) при x ® 0 (см. пример 15) и f=o (x 2) является функцией o (x) при x ® 0, найдем

Определение 19. Если f=o(g) при x® a и g(x) - бесконечно малая при x® a, то говорят, что f(x) - бесконечно малая более высокого по сравнению с g(x) порядка при x® a.

Пример 18. x²- бесконечно малая более высокого порядка по сравнению с x при x® 0

Определение 20. Если f(x), g(x) -бесконечно большие при x® a и f=o(g) при x® a, то говорят, что g - бесконечно большая более высокого порядка по сравнению с f.

Пример 19. Функции f=x 3 +x 2+2 x+ 1, g=x 4+3 x 2 -бесконечно большие при x® Ґ, и так как lim_{x® Ґ} f/g=0, то g — бесконечно большая более высокого порядка по сравнению с f

Отметим некоторые правила обращения с символами o(), O().