Теорема 4.1 (существование обратной функции)
Теорема 4.1 (существование обратной функции) Если функция y=f(x) возрастает (убывает) на множестве Х={х}, то на соответствующем множестве У={y} существует однозначная обратная функция х= §5. Предел функции п. 1. Предел функции при х → х0 Пусть функция у = f(x) определена на некотором множестве Х и точка х0 является предельной точкой этого множества, т.е. в окрестности точки х0 содержатся точки множества х, отличные от х0. Точка х0 может принадлежать множеству Х или не принадлежать ему => функция у = f(x) определена в точке х0, либо не определена. Например, если х = (а, в) и х = [а;b], то точки а и в – предельные и в первом случае они не принадлежат множеству х, а во втором – принадлежат. Возьмем из Х последовательность точек, отличных от х0: х1, …, хn, …(1), сходящуюся к х0. Значения функции в точках этой последовательности также образуют числовую последовательность f(х1), f(х2), …, f(хn) (2), по отношению к которой можно ставить вопрос о существовании предела. Опр. 5.1 (по Гейне) Число А называется пределом функции f(x) при х = х0 (х → х0), если для любой сходящейся к х0 последовательности (1) значений аргумента х ≠ х0, соответствующая последовательность (2) значений функции сходится к числу А (f(x) → А при х→ х0)
Функция f(x) может иметь в точке х0 только один предел. Это следует из того, что последовательность {f(хn)} имеет только один предел. Опр. 5.2 (по Коши) Число А называется пределом функции f(x) в точке х = х0, если для Так как неравенство, |f(x) – A| < Опр. 5.3. (ε-δ окрестности): Число А называется пределом функции f(x) в точке х = х0, если для Теорема 5.1. Определение предела функции по Гейне и по Коши эквивалентно.
П-2. Предел функции при х → х0 – 0 и при х → х0 + 0 (односторонние пределы). Опр.5.4 Число А называется правым (левым) пределом функции f(x) в точке х0, если для Правый и левый пределы называются односторонними пределами функции в точке.
Опр. 5.5 (ε – δ) число А называется правым (левым пределом) функции f(x) в точке х0, если
Теорема 5.2 Функция f(x) имеет предел в точке х0 <=> когда в этой точке п. 3. Предел функции при х → ∞, х → – ∞, х → + ∞. Опр. 5.6 Число А называется пределом функции f(x) при х → ∞, если для Опр. 5.7 Число А называется пределом функции f(x) при х → + ∞ (– ∞), если для Опр.5.8 Число А называется пределом функции f(x) при х → + ∞, если
п.4. Теории о пределах функции Теорема 5.3 Если функции f(x) и g(x) имеют в точке х0 пределы А и В, т.е.
1) 2) 3) 4) Теорема 5.4: Пусть функции Теоремы 5.3. и 5.4. верны также и в случае х0=+∞, -∞, ∞.
П-5. Замечательные пределы Первый замечательный предел
|

 (у), также возрастающая (убывающая).
(у), также возрастающая (убывающая).

 , такое, что для всех
, такое, что для всех 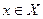 , х ≠ х0, удовлетворяющих неравенству | х - х0 | <
, х ≠ х0, удовлетворяющих неравенству | х - х0 | <  , выполняется неравенство |f(x) – A| <
, выполняется неравенство |f(x) – A| < 
 , то
, то - окрестности
- окрестности 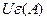 точки А найдется такие
точки А найдется такие  точки х0, что для
точки х0, что для 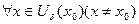 соответствующие значения f(x) принадлежат окрестности
соответствующие значения f(x) принадлежат окрестности 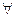 сходящихся к х0 последовательности (1), элементы которой больше (меньше) х0, соответствующая последовательность (2) сходится к А.
сходящихся к х0 последовательности (1), элементы которой больше (меньше) х0, соответствующая последовательность (2) сходится к А.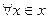
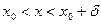 (
( ) выполняется
) выполняется .
. как правый, так и левый предел, и они равны. В этом случае предел функции равен односторонним пределам.
как правый, так и левый предел, и они равны. В этом случае предел функции равен односторонним пределам. (х > δ =>
(х > δ =>  ,
, 
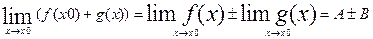


 , если В ≠ 0.
, если В ≠ 0. определены в некоторой окрестности точки х0, за исключением, быть может, самой точки х0, и функции f(x), h(x) имеют в точке х0 предел, равный А, т.е.
определены в некоторой окрестности точки х0, за исключением, быть может, самой точки х0, и функции f(x), h(x) имеют в точке х0 предел, равный А, т.е. 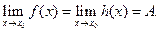 Пусть, кроме того, выполняются неравенства
Пусть, кроме того, выполняются неравенства  Тогда
Тогда  .
.



