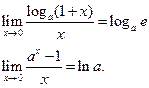Известно, что  . Докажем, что
. Докажем, что  .
.
П- 6. Б.б. и б.м. функции
Опр. 5.9. Функция 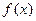 называется б.м. в точке х=х0
называется б.м. в точке х=х0 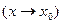 , если
, если 
Аналогично определяется б.м. функции при 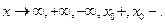
Теорема 5.6: Для того, чтобы число А было пределом функции f(x) в точке x0  , чтобы выполнялось равенство f(x)=A+α(x), где α(x)-б.м. при x→ x0
, чтобы выполнялось равенство f(x)=A+α(x), где α(x)-б.м. при x→ x0
Опр. 5.10 Функция  называется б.б. в т. x= x0 (x → x0), если ∀М >0 ∃ δ>0
называется б.б. в т. x= x0 (x → x0), если ∀М >0 ∃ δ>0
∀x ∈ X 0<|x- x0|<δ => |f(x)|>M. Тогда  .
.
Если же f(x)>M, тогда  .
.
f(x)<-M, тогда  .
.
Между б.м. и б.б. функциями существует аналогичная связь, как и между соответствующими последовательностями, т.е. если f(x) – б.б. при x→ x0, то  - б.м., при x→ x0 и наоборот.
- б.м., при x→ x0 и наоборот.
Если  и β(x) – б.м. при x→ x0 , то
и β(x) – б.м. при x→ x0 , то  называется неопределенностью типа
называется неопределенностью типа  . Если
. Если  и β(x) – б.б. при x→ x0 , то
и β(x) – б.б. при x→ x0 , то  называется неопределенностью типа
называется неопределенностью типа  ,
,  - β(x)=
- β(x)=  Аналогично вводятся неопределенности 0,
Аналогично вводятся неопределенности 0,  ,
,  ,
,  ,
,  Раскрыть неопределенность – значит найти предел соответствующего выражения(если он существует), что зависит от конкретных функций, входящих в выражение.
Раскрыть неопределенность – значит найти предел соответствующего выражения(если он существует), что зависит от конкретных функций, входящих в выражение.
Рассмотрим правила сравнения б.м. функций _  и β(x) – б.м. при x→ x0 . Тогда:
и β(x) – б.м. при x→ x0 . Тогда:
1) Если  =А
=А  , то функции
, то функции  и β(x) называются б.м. одного порядка.
и β(x) называются б.м. одного порядка.
2) Если  =1, то функции
=1, то функции  и β(x) называются эквивалентными б.м.
и β(x) называются эквивалентными б.м.
3) Если  =0, то функция
=0, то функция  называется б.м. более высокого порядка малости, чем β(x).
называется б.м. более высокого порядка малости, чем β(x).
4)  =А
=А  , то функция
, то функция  называется б.м. n-го порядка относительно β(x).
называется б.м. n-го порядка относительно β(x).
Теорема 5.7: Если при 
 и ∃
и ∃  то
то  причем
причем  .
.
Док-ть: 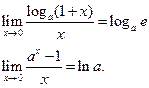
§6. Непрерывность функции в точке х0
Пусть функция f(x) определена в некоторой окрестности точки x0

 . Докажем, что
. Докажем, что  .
.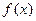 называется б.м. в точке х=х0
называется б.м. в точке х=х0 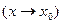 , если
, если 
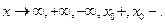
 , чтобы выполнялось равенство f(x)=A+α(x), где α(x)-б.м. при x→ x0
, чтобы выполнялось равенство f(x)=A+α(x), где α(x)-б.м. при x→ x0  называется б.б. в т. x= x0 (x → x0), если ∀М >0 ∃ δ>0
называется б.б. в т. x= x0 (x → x0), если ∀М >0 ∃ δ>0 .
. .
. .
. - б.м., при x→ x0 и наоборот.
- б.м., при x→ x0 и наоборот. и β(x) – б.м. при x→ x0 , то
и β(x) – б.м. при x→ x0 , то  называется неопределенностью типа
называется неопределенностью типа  . Если
. Если  называется неопределенностью типа
называется неопределенностью типа  ,
,  Аналогично вводятся неопределенности 0,
Аналогично вводятся неопределенности 0,  ,
,  ,
,  ,
,  Раскрыть неопределенность – значит найти предел соответствующего выражения(если он существует), что зависит от конкретных функций, входящих в выражение.
Раскрыть неопределенность – значит найти предел соответствующего выражения(если он существует), что зависит от конкретных функций, входящих в выражение. =А
=А  , то функции
, то функции  =А
=А 
 и ∃
и ∃  то
то  причем
причем  .
.