Непрерывность тригонометрических функций
Показать, что функция sin x непрерывна в любой точке х. Непрерывность cos x в любой точке х будет доказываться аналогично. Непрерывность функции sin x и cos x по теореме 6.1 => непрерывность функций tgx = Непрерывность функции f(x)=|x| f(x)=|x|= Эта функция определена непрерывна во всех точках числовой прямой. В точках полупрямой (0; В точках полупрямой (- Чтобы установить непрерывность функции |x| в точке х=0, вычислим односторонние пределы функции в этой точке:
Таким образом, пределы функции в точке х=0 слева и справа совпадают и равны значению функции в этой точке => функция |х| непрерывна в точке х=0 => непрерывна в любом х числовой прямой. Таким образом, рассмотренные функции непрерывны в любой точке, в окрестности которой они определены. На основании теоремы 5.1 о непрерывности Функция f(x) непрерывна в интервале (a,b), если она непрерывна в любой точке этого интервала; непрерывна на отрезке [a,b], если она непрерывна в интервале (a,b), непрерывна справа в точке а и слева в точке b, т.е.
|

 и sec x =
и sec x =  для любого х {x=
для любого х {x=  } и функций ctg x =
} и функций ctg x = 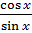 и cosec x =
и cosec x =  для любого х {x=
для любого х {x=  }
}
 ) она непрерывна, т.к. при х>0 f(x)=x;
) она непрерывна, т.к. при х>0 f(x)=x; ; 0) она непрерывна, т.к. при x>0, f(x)= - х и ее можно представить как произведение 2-х непрерывных функций (-1) и х и применить теорему 6.1 о непрерывности произведения
; 0) она непрерывна, т.к. при x>0, f(x)= - х и ее можно представить как произведение 2-х непрерывных функций (-1) и х и применить теорему 6.1 о непрерывности произведения =
= 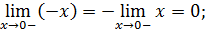
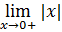 =
= 

 Р, П и Ч мы утверждаем, что функции, получаемые из них с помощью конечного числа арифметических действий, является также непрерывными функциями в любой точке, в окрестности которой они определены.
Р, П и Ч мы утверждаем, что функции, получаемые из них с помощью конечного числа арифметических действий, является также непрерывными функциями в любой точке, в окрестности которой они определены.




