Бюджетное ограничение. Бюджетная линия
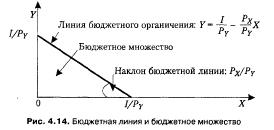
Возможности экономических субъектов далеко не безграничны, т. е. способность субъекта удовлетворять свои предпочтения определяются при помощи бюджетного ограничения. Бюджет индивида определяется доходом. Если предположить, что доход экономического субъекта расходуется на приобретение только двух товаров (X и У) по соответствующим ценам Рх и Ру то бюджетное ограничение можно выразить следующим образом: I ≥Рхх + Руу. Графически это условие можно проиллюстрировать в виде так называемого бюджетного множества
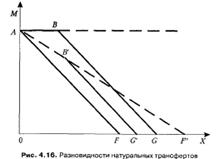
Если экономический субъект не делает сбережений и тратит весь свой доход на приобретение товаров, то формула бюджетного ограничения (бюджетного множества) превращается в уравнение бюджетной линии: I =Рхх + Руу. Бюджетная линия (линия бюджетного ограничения) — это геометрическое место точек, представляющих ряд всех возможных наборов благ (или единиц благ), доступных при данных ценах и доходах. Все товарные наборы, находящиеся в бюджетном множестве, доступны для потребителя, а вне данного множества (выше и правее) — недоступны. Наклон линии бюджетного ограничения представляет собой коэффициент при Х в формуле Ломаные линии бюджетных ограничений 1. Натуральные трансферты(а).
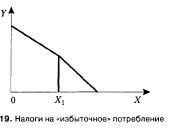
2. Получение скидки или повышение тарифа(б)
3. Бюджетное гос.ограничение(в)
|
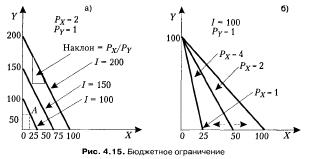
. Он имеет отрицательное значение, что свидетельствует о наклоне линии бюджетного ограничения. Наклон бюджетной линии показывает пропорцию, в которой рынок готов «заместить» товар У товаром X.
