Билет № 51. Производная. Производной функцией
При
Параллелепипед — это призма, основание которой —параллелограмм. Параллелепипед имеет шесть граней и все они параллелограммы. Противоположные грани попарно равны и параллельны. Параллелепипед имеет четыре диагонали. Все диагонали Параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Основанием параллелепипеда может быть любая грань.
Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед, у которого все шесть граней прямоугольники называется прямоугольным. Прямоугольный параллелепипед, все грани которого квадраты, называется кубом. Все ребра куба равны. Билет № 6 Правила вычисления производной. Производная суммы и разности Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций: 1. (f + g)’ = f ’ + g ’ 2. (f − g)’ = f ’ − g ’
|
в точке 
называется число, к которому стремится разностное отношение
, стремящемся к нулю, где 
– приращение аргумента в точке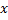 
- производная точка, лежащая в некоторой окрестности фиксированной точки 
2. Параллелепипед. Прямоугольный параллелепипед.
