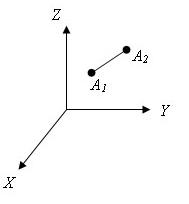
Декартовые координаты в пространстве.
Прямые x, y, z называются координатными осями (или осями координат),
Билет № 8 Производная тригонометрических функций. Для нахождения производных от тригонометрических функций применяют следующие правила дифференцирования: 2. Расстояние между точками в пространстве.
Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2)
Билет № 9 1. Первообразные. Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x) выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx
Пример 1. Найти производную функции Решение:
Ответ:
Пример 2. Найти Решение: По правилу дифференцирования дроби имеем:.
Ответ:
Пример 3. Чему равен тангенс угла наклона касательной к графику функции у = х2 + 2, в точке хо = – 1. Решение: Тангенс угла наклона касательной к графику функции есть значение производной данной функции в точке хо.
Ответ: – 2.
|

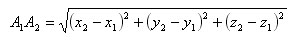

 .
. .
. .
.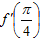 , если
, если  .
. .
.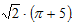
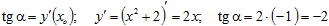 .
.


