Система взаимосвязанных индексов, факторный анализ.
Система взаимосвязанных индексов позволяет применять индексный метод для изучения взаимосвязей общественных явлений с целью определения влияния факторов на изменение сложного явления. Между отдельными индексам существуют взаимосвязи, позволяющие на основе одних индексов определять другие. Одной из таких взаимосвязей является взаимосвязь индексов связанных явлений. Большинство экономических явлений, изучаемых с помощью индексов, связаны между собой. Между индексами этих явлений существует точно такая же взаимосвязь. В общем виде эта взаимосвязь выглядит так:
В абсолютном выражении ∆xd = ∆х + ∆d
Например, т.к. товарооборот - это произведение цены на количество товара, то и индекс товарооборота равен произведению индексов цен и физического объема товарооборота
В абсолютном выражении эта взаимосвязь: ∆pq=∆p+∆q
Аналогично определяется взаимосвязь и других индексов связанных явлений. Рассмотрим некоторые особые взаимосвязи: Индекс затрат труда равен индексу трудоемкости умноженному на индекс физического объема продукции: lT=It-Iq т.к. T=tq,
∆T=∆t +∆q
(1.9.27) Индекс объема продукции равен индексу производительности труда умноженному на индекс затрат труда: I, =IW- It т.к. q = wT;
∆q=∆w+∆T
Решение типовых задач по теме 1.9.
|
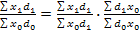(1.9.24)
(1.9.25)
(1.9.26)
(1.9.28)
(1.9.29)
