Базисные и цепные индексы.
При изучении динамики явления за ряд последовательных периодов (лет, месяцев т.д.) рассчитывают ряд индексов. Эти индексы показывают изменение явления либо по отношению к постоянной базе (базисные индексы), либо по отношению к переменной базе (цепные индексы). Цепные и базисные индексы могут быть индивидуальными и общими. Расчет индивидуальных индексов при этом прост, (Для удобства записи отсчет времени начнем с первого периода). Тогда качественные базисные индивидуальные индексы в общем виде
И т.д. а цепные
ит.д. Аналогично рассчитываются и количественные базисные и цепные индивидуальные индексы. Взаимосвязь между ними: произведение цепных индексов равно последнему базисному:
При построении базисных и цепных общих индексов возникает проблема весов. Веса при этом могут быть постоянными (т.е. одинаковыми во всех индексах) и могут быть переменными (т.е. изменяющимися от индекса к индексу). В большинстве случаев принято все общие индексы (базисные и цепные) количественных показателей записывать с постоянными весами. В общем виде это выглядит так:
И т.д. и цепные индексы
и т.д. Взаимосвязь между ними в этом случае сохраняется: произведение цепных индексов равно последнему базисному индексу:
Базисные и цепные индексы качественных показателей в большинстве случаев записываются с переменными весами. В общем виде это будет: базисные индексы:
И т.д. и цепные индексы
и т.д. Между базисными и цепными индексами с переменными весами вышеуказанная взаимосвязь отсутствует. Конкретные базисные и цепные индексы в приложении I (Таблица 2).
|

 ,
, 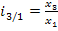 ,
,  (1.9.16)
(1.9.16)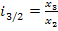 ,
,  (1.9.17)
(1.9.17) =
=  (1.9.18)
(1.9.18)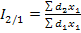 ,
,  ,
,  (1.9.19)
(1.9.19)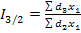 ,
,  (1.9.20)
(1.9.20) (1.9.21)
(1.9.21) ,
,  ,
,  (1.9.22)
(1.9.22) ,
,  (1.9.23)
(1.9.23)


