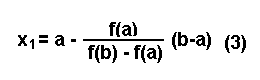Вопрос численное решение нелинейных скалярных уравнений. Метод хорд.

 

Метод хорд иногда называют способом пропорциональных частей. Данный способ является более быстрым способом нахождения корня уравнения F(x) = 0 (1) на отрезке [a,b], чем метод деления отрезка пополам. Напомним, что для отрезка [a,b] должно выполняться условие F(a)*F(b) < 0.

Пусть для определённости f(a) < 0 и f(b) > 0. Тогда, вместо того чтобы делить отрезок [a,b] пополам, более естественно разделить его в отношении - f(a): f(b).

Это даёт нам приближённое значение корня x1 = a + h1, (2)
где h1 = -f(a)(b-a)/(-f(a) + f(b)) = f(a)(b-a)/(f(b) + f(a)) (2)

Далее, применим этот приём к тому из отрезков [a, x1] или [ x1, b], на концах которого функция имеет противоположные знаки, получим второе приближение корня и так далее.

Геометрически способ пропорциональных частей эквивалентен замене кривой y=f(x) хордой, проходящей через точки A[a,f(a)] и B[b,f(b)] (рис. 1). Отсюда и название метода.

 

рис. (1)

В самом деле, уравнение хорды АВ есть

Отсюда, полагая и, получим:

Формула (3) полностью эквивалентна формулам (1) и (2).

 

рис. 2

Результаты математических исследований показывают, что при применении метода хорд получаем сходящуюся последовательность хорд, один конец которых неподвижен, например, как на рис. 2, причем:
1. неподвижен тот конец, для которого знак функции f(x) совпадает со знаком её второй производной f ''(x);
2. последовательные приближения лежат по ту сторону корня x, где функция f(x) имеет знак противоположный знаку её второй производной f ''(x).

Точные математические исследования показывают, что

то есть так как мы используем для вычислений компьютер, то процесс вычислений будет считаться законченным тогда, когда следующее значение корня будет отличаться от предыдущего на малое число d, которое будет показывать нам точность вычислений.