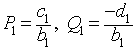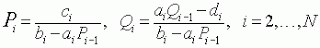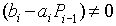Метод прогонки
Метод прогонки для решения систем линейных алгебраических уравнений(СЛАУ).
Часто при решении задач математической физики(например краевая задача для обыкновенных дифференциальных уравнений 2-го порядка) встречаются матрицы, в которых большинство элементов равно нулю. Причем структура матрицы не хаотична, а вполне определена, а именно - матрица трехдиагональна, ненулевые элементы расположены на главной диагонали и двух прилегающих к ней.
Метод прогонки является частным случаем метода Гаусса, и также состоит из прямого и обратного хода. Для решения системы, матрицу сначала нужно привести к двухдиагональной:
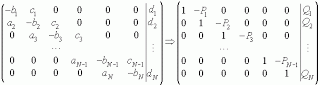
Поделив первую строку матрицы, приведенной выше, на -b1 очевидно, что:
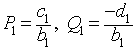
и можно вывести формулу для прямого хода: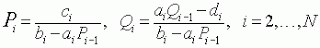 
Затем необходимо выполнить обратный ход - найти вектор X, из последней строки преобразованной матрицы следует, что xn= Qn.
В тоже время остальные элементы вектора считаются по формуле:
Следует заметить, что метод устойчив если(следует из диагонального преобладания матрицы А):
и корректен, если(иначе формулы прямого хода не имеют смысла):
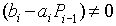
Вопрос численное решение системы нелинейных алгебраических уравнений метод простой итерации
