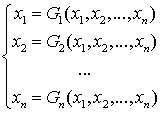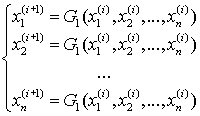Системы нелинейных уравнений
При решении задач моделирования поведения химических систем достаточно часто приходится решать системы уравнений, нелинейных по отношению к переменным. Системы n линейных уравнений с n неизвестными x 1, x 2 ,..., xn в общем случае принято записывать следующим образом:
где F 1, F 2 ,…, Fn – любые функции независимых переменных, в том числе и нелинейные относительно неизвестных. Как и в случае систем линейных уравнений, решением системы является такой вектор (или векторы) (X*), который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно. Рассмотрим несколько простейших итерационных методов решения систем нелинейных уравнений, а именно, метод простой итерации, метод Зейделя и метод Ньютона. Метод простой итерации Для реализации этого метода решаемую систему уравнений необходимо путем алгебраических преобразований привести к следующему виду, выразив из каждого уравнения по одной переменной следующим образом:
Выбирая затем вектор начального приближения , подставляют его в преобразованную систему уравнений. Из первого уравнения получают новое приближение к первой переменной, из второго – второй и т. д. Полученное уточненное значение переменных снова подставляют в эти уравнения и т.д.Таким образом, на (i+1)-м шаге итерационной процедуры имеем
|