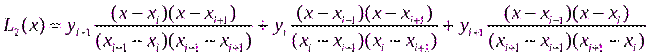Графическая иллюстрация метода наименьших квадратов (мнк).
На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это
Для чего это нужно, к чему все эти аппроксимации? Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта. Вопрос При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений. Высокой степени многочлена можно избежать, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Простейшим, часто используемым видом локальной интерполяции, является кусочно-линейная интерполяция. Она состоит в том, что заданные точки
Для каждого из Формулы (1) и (2) эквивалентны. В случае кусочно-квадратичной интерполяции в качестве интерполяционной функции на отрезке (
где Для определения неизвестных коэффициентов
|

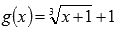 , розовые точки – это исходные данные.
, розовые точки – это исходные данные.
 (
( ) соединяются прямолинейными отрезками, а функция
) соединяются прямолинейными отрезками, а функция 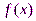 приближается к ломаной с вершинами в данных точках.
приближается к ломаной с вершинами в данных точках.
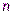 интервалов
интервалов  , (
, ( ) в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки
) в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки 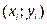 ,
, 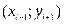 :
: (1)
(1)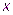 , затем подставить значение
, затем подставить значение 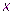 в формулу (1) для найденного интервала и найти приближенное значение функции
в формулу (1) для найденного интервала и найти приближенное значение функции 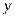 . Можно показать, что интерполирование по формуле (1) тождественно интерполированию с помощью интерполяционного многочлена Лагранжа первой степени (
. Можно показать, что интерполирование по формуле (1) тождественно интерполированию с помощью интерполяционного многочлена Лагранжа первой степени (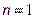 ) для точек
) для точек 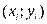 ,
,  :
: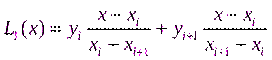 (2)
(2)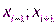 ) принимается квадратичный трехчлен:
) принимается квадратичный трехчлен: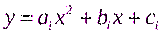 , (3)
, (3) .
. необходимы три уравнения. Ими служат условия прохождения параболы через три точки
необходимы три уравнения. Ими служат условия прохождения параболы через три точки 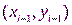 ,
,  ,
,  . Эти условия можно записать в виде:
. Эти условия можно записать в виде: (4)
(4) проводится по трем ближайшим точкам. Решив систему (4) относительно
проводится по трем ближайшим точкам. Решив систему (4) относительно  , и подставив найденные значения в уравнение (3), получим интерполяционный многочлен Лагранжа второй степени (
, и подставив найденные значения в уравнение (3), получим интерполяционный многочлен Лагранжа второй степени (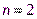 ) для трех соседних точек
) для трех соседних точек 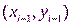 ,
, 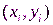 ,
, 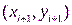 :
: