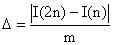Вопрос численное интегрирование метод Симпсона оценки точности численого определения интеграла
Интегрирование по методу Симпсона. Формула трапеций дает результат, сильно зависящий от величины шага h, что сказывается на точности вычисления определенного интеграла особенно в тех случаях, когда функция имеет немонотонный характер. Можно предположить повышение точности вычислений, если вместо отрезков прямых, заменяющих криволинейные фрагменты графика функции f(x), использовать, например, фрагменты парабол, проводимых через три соседних точки графика. Подобная геометрическая интерпретация лежит в основе метода Симпсона для вычисления определенного интеграла. Весь интервал интегрирования [ a,b ] разбивается на четное число одинаковых отрезков n, длина отрезка также будет равна h=(b-a)/n. Формула Симпсона имеет вид:
В формуле выражения в скобках представляют собой суммы значений подынтегральной функции соответственно на концах нечетных и четных внутренних отрезков. Остаточный член формулы Симпсона пропорционален уже четвертой степени шага
Для вычисления определенного интеграла методом Симпсона также несложно составить процедуру-функцию с параметрами, аналогичными параметрам функции, реализующей метод трапеций. В формулах для оценки погрешности квадратурных формул R используются значения производных подинтегральной функции, что требует дополнительного анализа и вычислений. В связи с этим получило распространение практическое правило Рунге оценки погрешности. Пусть
Необходимо определить, с какой точностью вычислен итеграл I(2n), т.е. найти абсолютную погрешность
Для непосредственно определения данной погрешности необходимо найти максимум модуля соответствующей производжной от интегрируемой функции на отрезке [a, b]. Часто это достаточно трудоемкий или вообще невозможный процесс. Напрмер если интегрируемая функция задана таблично. В таких случаях оценку погрешности
Здесь m = 3 для методов средних прямоугольников и трапеций, m = 15 для метода Симпсона. Вопрос
|
величины I(2n) можно провести следующим образом:
