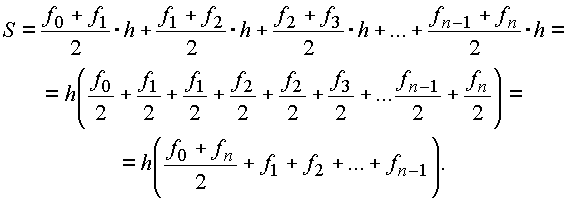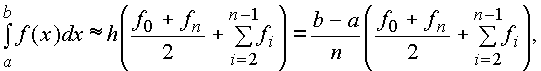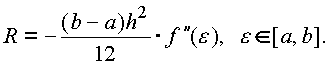Вопрос численное интегрирование метод трапеций метод Рунге оценки точности численого определения интеграла
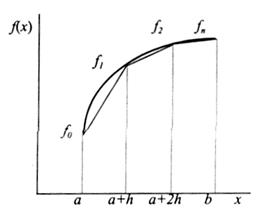
Метод трапеций для оценки определенного интеграла. Величина определенного интеграла численно равна площади фигуры, образованной графиком функции и осью абсцисс (геометрический смысл определенного интеграла). Следовательно, найти Для решения задачи разобьем интервал [ a,b ] на n одинаковых участков. Длина каждого участка будет равна h=(b-a)/n (см. рис.).
Восстановим перпендикуляры из каждой точки до пересечения с графиком функции f(x). Если заменить полученные криволинейные фрагменты графика функции отрезками прямых, то тогда приближенно площадь фигуры, а следовательно и величина определенного интеграла оценивается как площадь всех полученных трапеций. Обозначим последовательно значения подынтегральных функций на концах отрезков f0, f1, f2,..., fn и подсчитаем площадь трапеций
В общем случае формула трапеций принимает вид
где fi – значение подынтегральной функции в точках разбиения интервала (a,b) на равные участки с шагом h; f0, fn – значения подынтегральной функции соответственно в точках a и b. Остаточный член пропорционален длине интервала [ a,b ] и квадрату шага h
Согласно рис. и формуле остаточного члена, точность вычисления определенного интеграла повышается с уменьшением шага h (увеличением числа отрезков n). Метод трапеций можно реализовать в виде процедуры или даже функции, поскольку результат вычисления определенного интеграла – скалярная величина. Параметрами программного модуля являются границы интервала (a и b) и число шагов разбиения на малые интервалы n. Для составления универсальной функции целесообразно предусмотреть вычисление подынтегральной функции f(x) во внешней процедуре – функции. Правило Рунге — правило оценки погрешности численных методов, было предложено К. Рунге в начале 20 века.[1] Основная идея (для методов Рунге-Кутты решения ОДУ) состоит в вычислении приближения выбранным методом с шагом h, а затем с шагом h/2, и дальнейшем рассмотрении разностей погрешностей для этих двух вычислений.
|

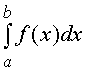 – это значит оценить площадь фигуры, ограниченной перпендикулярами, восстановленными к графику подынтегральной функции f(x) из точек a и b, расположенных на оси аргумента x.
– это значит оценить площадь фигуры, ограниченной перпендикулярами, восстановленными к графику подынтегральной функции f(x) из точек a и b, расположенных на оси аргумента x.