Метод Зейделя для решения СЛАУ

Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.

Итерации по методу Зейделя отличаются от простых итераций (10.12) тем, что при нахождении i-й компоненты (k+1)-го приближения сразу используются уже найденные компоненты (к +1) -го приближения с меньшими номерами . При рассмотрении развернутой формы системы итерационный процесс записывается в виде

 

В каждое последующее уравнение подставляются значения неизвестных, полученных из предыдущих уравнений.

Теорема (10.3) о достаточном условии сходимости метода Зейделя. Если для системы какая-либо норма матрицы меньше единицы, т.е. , то процесс последовательных приближений (10.15) сходится к единственному решению исходной системы при любом начальном приближении .

Записывая (10.15) в матричной форме, получаем

(10.16)

где являются разложениями матрицы

Преобразуя (10.16) к виду , получаем матричную форму итерационного процесса метода Зейделя:

(10.17)

Тогда достаточное, а также необходимое и достаточное условия сходимости будут соответственно такими (см. теоремы 10.1 и 10.2):
Замечания 10.8

1. Для обеспечения сходимости метода Зейделя требуется преобразовать систему к виду с преобладанием диагональных элементов в матрице а (см. метод простых итераций).

2. Процесс (10.15) называется последовательным итерированием, так как на каждой итерации полученные из предыдущих уравнений значения подставляются в последующие. Как правило, метод Зейделя обеспечивает лучшую сходимость, чем метод простых итераций (за счет накопления информации, полученной при решении предыдущих уравнений). Метод Зейделя может сходиться, если расходится метод простых итераций, и наоборот.

3. При расчетах на ЭВМ удобнее пользоваться формулой (10.16).

4. Преимуществом метода Зейделя, как и метода простых итераций, является его "самоисправляемость".

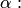
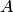5. Метод Зейделя имеет преимущества перед методом простых итераций, так как он всегда сходится для нормальных систем линейных алгебраических уравнений, т.е. таких систем, в которых матрица является симметрической и положительно определенной. Систему линейных алгебраических уравнений с невырожденной матрицей всегда можно преобразовать к нормальной, если ее умножить слева на матрицу (матрица 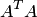— симметрическая). Система является нормальной.

Алгоритм метода Зейделя

1. Преобразовать систему к виду одним из описанных способов.

2. Задать начальное приближение решения произвольно или положить , а также малое положительное число (точность). Положить .

3. Произвести расчеты по формуле (10.15) или (10.16) и найти .

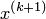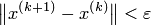4. Если выполнено условие окончания , процесс завершить и в качестве приближенного решения задачи принять . Иначе положить и перейти к пункту 3.

Пример 10.15. Методом Зейделя с точностью решить систему линейных алгебраических уравнений:

 

Решение. 1. Приведем систему к виду (см. пример 10.14):

Так как , условие сходимости выполняется.

2. Зададим . В поставленной задаче .

Выполним расчеты по формуле (10.15): и результаты занесем в табл. 10.6.

Очевидно, найденное решение является точным.

4. Расчет завершен, поскольку выполнено условие окончания .

Пример 10.16. Методом Зейделя с точностью решить систему линейных алгебраических уравнений:

 

Решение. Так как , в данной системе диагональные элементы преобладают. Выразим из первого уравнения 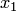, из второго , из третьего

2. Зададим . В поставленной задаче .

3. Выполним расчеты по формулам (10.15): и результаты занесем в табл. 10.7.

Очевидно, найденное решение является точным.

4. Расчет завершен, поскольку выполнено условие окончания .