Метод простых итераций
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В таких случаях более эффективным способом численного решения уравнений является метод итерации. Пусть дано уравнение (1) Заменим его равносильным уравнением Здесь Вычислительная формула метода простых итераций: Если последовательность
Первый способ приведения AX = B к виду (9) Предполагая, что где
При таком способе получения уравнения (9) справедливо следствие из теоремы 1, определяющее условие сходимости итерационного процесса.
Выражение (12) означает, что в матрице A в каждой строке диагональный элемент по модулю больше суммы модулей остальных элементов строки. Если данное условие не выполняется, необходимо соответствующим образом преобразовать СЛАУ. Это можно сделать, выполнив эквивалентные преобразования системы: перестановка строк; линейная комбинация строк. Пример. Дана система уравнений. Привести ее к виду, пригодному для решения методом простых итераций первым способом. Условие (12) не выполняется ни в одной из строк. Поместим строку (c) на первое место: Теперь для первой и третьей строки условие (12) выполняется. В качестве третьей строки возьмем линейную комбинацию (c) – (a): Данную систему уже можно приводить к виду (9): Т.о. В качестве нулевого приближения примем Второй способ приведения AX = B к виду (9) В предыдущем способе обязательным условием являлось выполнение неравенства (12). Во многих случаях это далеко не просто. Во втором способе любую невырожденную систему уравнений AX = B всегда можно заменить эквивалентной системой так, что условие сходимости будет выполняться. Для этого умножим уравнение AX = B на матрицу D = А –1 – , где – матрица с малыми по модулю элементами. Последовательно получим: Обозначим В результате получим систему вида Очевидно, что если элементы матрицы выбрать достаточно малыми по модулю, то можно обеспечить выполнение условия Т.е. для сходимости итерационного процесса необходимо выполнение условия
|

 .
. . (9)
. (9) ;
;  .
. . (10)
. (10) имеет предел
имеет предел  , то этот предел является решением системы (10).
, то этот предел является решением системы (10). , то система уравнений (9) имеет единственное решение и итерационный процесс (10) сходится к решению независимо от начального приближения.
Критерий окончания итерационного процесса:
, то система уравнений (9) имеет единственное решение и итерационный процесс (10) сходится к решению независимо от начального приближения.
Критерий окончания итерационного процесса: 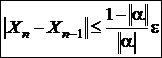 .
Здесь - заданная точность вычислений. В качестве решения берется величина Xn.
.
Здесь - заданная точность вычислений. В качестве решения берется величина Xn.
 разрешим первое уравнение системы (1) относительно
разрешим первое уравнение системы (1) относительно  , второе – относительно
, второе – относительно  ,, n ‑-ое уравнение – относительно
,, n ‑-ое уравнение – относительно  . В результате получим
. В результате получим , (11)
, (11) ;
;  при
при  . Система (9) в матричной форме имеет вид (9).
. Система (9) в матричной форме имеет вид (9). метод итераций сходится, если выполнены неравенства
метод итераций сходится, если выполнены неравенства
 ,
,  . (12)
. (12)
 .
. .
. .
.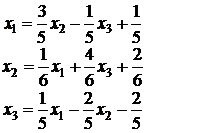 .
. ,
,  .
.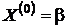 .
. ;
;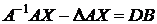 ;
; .
. ;
;  .
. .
. .
. или
или  .
.


