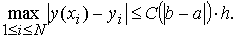Метод Эйлера для решения системы диф. уравнений. Запись уравнения Эйлера.

Если задачу об отыскании решений дифференциального уравнения удаётся свести к конечному числу алгебраических операций, операций дифференцирования и интегрирования известных функций, то говорят, что дифференциальное уравнение интегрируется в квадратурах.

В приложениях крайне редко встречаются уравнения. интегрируемые в квадратурах. Для исследования и решения уравнений, которые не интегрируются в квадратурах, используются численные методы решения задачи Коши.

 

Численное решение задачи Коши y' = f (x, y), y (a) = y ₀ на отрезке [ a, b ] состоит в построении таблицы приближённых значений y ₀, y ₁,..., y _i,..., y _N решения y = y (x), y (x_i) ≈ y _i,

в узлах сетки a = x ₀< x ₁<...< x _i <...< x _N = b. Если x _i = a + ih, h = (b-a)/ N, то сетка называется равномерной.

 

Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке x ₀ + h используется информация о решении только в точке x ₀.

Простейший одношаговый метод численного решения задачи Коши — метод Эйлера. В методе Эйлера величины y _i вычисляются по формуле: y _{i +1} = y_{i + h · f (xi, yi):}

y' = f (x, y), y (a) = y ₀, x ∈ [ a, b ],

x _i = a + ih, h = (b-a)/ N, i = 0,1, 2,..., N,

y (x_i)≈ y _i,

y _{i +1} = y_i + h · f (x_i, y_i).

Для погрешности метода Эйлера на одном шаге справедлива оценка

а для оценки погрешности решения на всём отрезке [ a, b ] справедливо

 

Для практической оценки погрешности можно рекомендовать правило Рунге: производятся вычисления с шагом h — вычисляются значения y ^(h) _i, затем производятся вычисления с половинным шагом h /2 — вычисляются значения y ^{(h /2)} _i.

 

За оценку погрешности вычислений с шагом h /2 принимают величину

 

Если соединить точки (x_i, y_i) прямолинейными отрезками, получим ломаную Эйлера — ломаную линию, каждое звено которой с началом в точке (x_i, y_i) имеет угловой коэффициент, равный f (x_i, y_i).

39. Кривые (кинетические кривые):

Графическое изображение зависимости концентрации реагентов от времени есть кинетическая кривая.

40. Критерии выбора адекватности модели:
Проверка адекватности модели состоит в сравнении дисперсий модельных и экспериментальных результатов и принятии или отклонении проверяемой гипотезы. В случае непринятия гипотезы осуществляется возврат к этапу 3 (получение математической модели кинетики химической реакции) для проработки следующей гипотезы по всем рассмотренным этапам.