Песталоцци;. а) -3cosx+с; б) 3sinx+с; в)3cosx ; г)0.
а) -3cosx+с; б) 3sinx+с; в)3cosx
а) -3cosx+с; б) 3sinx+с; в)3cosx
а) 12х+с; б)2x3+с; в)
а) 4+с; б) -
а) х2+с; б)
а) 4х--1+с; б) -
а) ex+1+с; б)0; в) 1.Вычислите площадь фигуры ограниченной линиями: у = х2+3х-4, у=0. а) - 6 Вычислите площадь фигуры ограниченной линиями: у=х2-3х, у=0. а)22 у=х2+3х, у=0. а) -4 Вычислите площадь фигуры ограниченной линиями: у =3х2-6х, у=0. а) 4 Вычислите площадь фигуры ограниченной линиями: у=х2+2х, у=0, а)3 Вычислите площадь фигуры ограниченной линиями: у =(х+1)2 ,у=5-х, у=0, а) - 6 Вычислите площадь фигуры ограниченной линиями: у=х2, у = 2х-х2, у=0. а)4; б) - 1 Вычислите площадь фигуры ограниченной линиями: у =(х+1)2 , у=1-х, у=0. а) - Вычислите площадь фигуры ограниченной линиями: у=4-х2 ,у=х+2, у=0, а) 1 у=4х - х2 ,у=4-х, у=0. а)6 Вычислите площадь фигуры ограниченной линиями: у=х2+1, у=х+3. а) -1
у=х2, у = 2х-х2 а) у =(х-2)2 ,у = -х2+8х-12. а) - 10
у=4-х2,у=х+2. а) 5; б)6
у =(х+3)2 , у = - х2-2х+3. а) 2 у =(х+2)2 ,у=х+2, а) 1
2.Вычислите интеграл:
а)2; б) 3; в)
а)9; б) 7; в)
а)5; б)
а)3; б)
а)2; б) 10; в)
а)0; б) -1; в)
а)0; б) -1; в)
а)18; б) 3; в)
а)8; б)
а)
а) 8ln4; б) 4ln2 -
а)5; б)3; в) 9;г)4.
а) 2; б)
а) 1; б) 2e +1; в)e; г)e - 1.
а)
а)27; б) 64; в)20; г) 0.
а)
а)
а)
а)
а) -
а)
а) 1; б)
а) -
а) е; б)
а)
Составьте уравнение касательной, проведенной к графику функции у=x – 3x2 в точке х0=2. а)y= - 11x - 10; б)y = 13x + 10; в)y = -10x - 22; г)y = 4x + 13. Составьте уравнение кривой, проходящей через точку М(1;4), если угловой коэффициент касательной к кривой в каждой ее точке равен 3х2-2х. а)y= x3 +x2+4; б)y = 6x - 2; в)y = 10x3– 2x2; г)y = 4x + 13. Точка движется прямолинейно с ускорением, а=12t2+6t. Найдите закон движения точки, если в момент времени t=1с. ее скорость v=8м/с, а путь s=6м. а)s= t3 +t2+4;б)s = 24t +6; в)s = 24t; г)s = t4 +t3 +t + 3. При каком значении α векторы а= 3i-5j+ᾳk и в= -4i-2j+k перпендикулярны? а)2; б) -2; в)22; г) -22. Тело брошено с поверхности земли вертикально вверх со скоростью v=(29,4- 9,8t)м/с. Найдите наибольшую высоту подъема тела. а)3; б) 44,1; в)19,6; г) 68. Найдите наибольшее и наименьшее значение функции в заданном промежутке, если у= а) -4,5 –наименьшее значение, б) -4 –наименьшее значение, в)-13,5 –наименьшее значение, г)0 –наименьшее значение,
2.Площадь осевого сечения цилиндра равна 81см2 . Найдите площадь полной поверхности цилиндра, если длина его образующей и длина диаметра основания равны. а)324 Найдите функцию, дифференциал которой равен (5х-2) а)y= x3 +x2+4; б )y = 5 3.Найдите длину радиуса шара, равновеликого цилиндру радиуса 6см и высотой 3см. Даны три вершины прямоугольника А(1;4;2;), В(2;-1;5), С(0;-2;4) прямоугольника АВСД. Найдите координаты вершины Д. Диагонали ромба 12см и 16см. Точка М, расположенная вне плоскости ромба, удалена от всех сторон ромба на 8см. Определите расстояние от точки М до плоскости ромба. а)2; б) -2; в)22; г) -22.
Составьте уравнение линии, если угловой коэффициент касательной в любой точке касания равен а)у =2; б)у =х+с; в)у = х; г) у=хс.
Ускорение движения тела, а= 24t2+8. Найдите закон движения тела, если в момент t=1с. Скорость тела v=10м/с, а путь равен12м. а)s=8t3+8t- 6;б) s=8t3+8t+c; в)s=2t4+4t2+c г) s=2t4+4t2+6 Стороны основания прямоугольного параллелепипеда6см и 8см, а длина диагонали параллелепипеда равна 26см. Найдите высоту параллелепипеда и площадь диагонального сечения. а)24см;240см2 б)28см,280см2; в)10см, 80см2; г)8см, 48см2. Скорость движущегося тела равна v=(4t-t2)м/c. Вычислите путь пройденный телом от начала движения до остановки. а)s=2t2 - Из некоторой точки пространства проведены к данной плоскости перпендикуляр, равный6см, и наклонная длиной 9см.Найдите длину проекции наклонной на данную плоскость. а)3; б) Скорость движущейся точки задана формулойv=2t-3(м/с).Найдите закон движения точки, если к моменту начала отсчета она прошла путь 6м. а)s=2t3-3t- 6;б) s=2; в) s=2t2 - 3t+c г) s=t2– 3t +6 Найдите уравнение кривой, если угловой коэффициент касательной в каждой ее точке равен 2х. а)у =2; б) у =х2+с; в)у = х2; г) у=хс.
3. Образующая конуса составляет с плоскостью основания угол в 450 . Найдите площадь полной поверхности конуса и объем, если его высота равна 6 см. а)v =72 в)v =72 Диаметр основания конуса равен 40, а длина образующей25. Найдите высоту конуса. а)15; б)32; в)26; г)
В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что ДД1=3, АВ =6, ВС =6. Найдите длину диагонали АС1. а)12; б) 9; в)69; г)
Диаметр основания конуса равен 24, а длина образующей - 13. Найдите высоту конуса. а)12; б)13; в)5 г)
Диаметр основания конуса равен 10, а длина образующей - 13. Найдите высоту конуса. а)12; б)13; в)269; г) Диаметр основания конуса равен 14, а длина образующей - 25. Найдите высоту конуса. а)12; б) 14; в)269; г) В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что АА1=10, АВ =5, А1Д1 =10. Найдите длину диагонали ДВ1. а)15; б)5; в)17; г) В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что ВВ1=9, АВ =12, АД =8. Найдите длину диагонали ВД1. а)12; б)127; в)17; г) В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что ДД1=6, СД =17, АД =6. Найдите длину диагонали АС1. а)12; б)24; в)17; г) Площадь боковой поверхности цилиндра равна 28 а) Площадь боковой поверхности цилиндра равна 18 а)9; б)18; в)20; г)4,5. В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что СА1=23, СД =3, АД =14. Найдите длину ребра ВВ1. а) В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что СА1=11, С1Д1 =2, АД =6. Найдите длину ребра СС1. а)9; б)6; в)12; г)161. В прямоугольном параллелепипеде АВСДА1В1С1Д1известно, что ДВ1=21, СД =16, В1С1 =11. Найдите длину ребра ВВ1. а)32; б) 8; в)22; г)19. Стороны основания правильной четырехугольной пирамиды равны 14, боковые ребра раны 25. Найдите площадь поверхности этой пирамиды. а)1348; б)196; в)672; г) 868. Стороны основания правильной четырехугольной пирамиды равны 6, боковые ребра раны 5. Найдите площадь поверхности этой пирамиды. а)36; б)48; в)84; г)96.
Песталоцци; 5. Гербарт 37. И.Г. Песталоццидің білім берудің жасаған теориясы:
38. И.Г. Песталоццидің элементарлық білім беру теориясы жетелейді:
39. Песталоццидің педагогикалық теориясы мен тәжірибесінде қарастырлатың жағдай:
40. И.Ф. Гербартің тәрбие үдерісінде ажыратылатың үш бөлімі:
41. Гербарт оқытудың негізгі міндетің көрсетеді:
42. Гербартиандық педагогиканың балаларды басқару жүйесі бағытталады: 1. балалардың өнерпаздық дамуына; 2. мұғалім мен балалардың қызметтестігін іске асыруға; 3. оқушылардың бастамасын мадақтауға; 4. балалардың дербестігін басуға; 5. саналы тәртіпті тәрбиелеуге 43. А..Ф. Дистервегтің педагогикалық теориясының негізіндеғі идея: 1. табиғи және еркін тәрбиелеу; 2. элементарлық тәрбиелеу; 3. жалпы адамша тәрбиелеу; 4. жалпы барлығын оқыту; 5. үйлесімді оқыту 44. А. Дистервегтің талабы бойынша, балаларда өнерпаздық даму дегенде түсінген: 1. көркем өнерпаздыққа қатысу; 2. белгілі мақсатқа жету бойынша өнерпаздық;; 3. сұрақтарды шешуде дербестік; 4. пікірде дербестік; 5. өзін-өзі тәрбиелеу, өзін-өзі жетілдіру 45. Француз ағартушыларын біріктірді идеялары: 1. жеке адамды жан-жақты және үйлесімді даму идеясы; 2. оқытуды өнімді еңбекпен ұштастыру идеясы; 3. мұғалім мен оқушының қарым-қатынас жасау идеясы; 4. қоғамдық тәрбие идеясы; 5. тәрбиенің халықтық идеясы 46. “Дамытушылық оқыту” идеясын ұсынған педагог: 1. Я.А. Коменский; 2. Дистервег; 3. Песталоцци; 4. Руссо; 5. Локк 47. Жеке адамды табиғат аясында, табиғи жағдайда тәрбиелеу міндеттін ұсынған педагог: 1. Песталоцци; 2. Гельвеций; 3. Руссо; 4. Коменский; 5. Штейнер 48. Сынып – сабақ жүйесінің негізгі белгілері: 1. белгілі бағдарлама бойынша оқушылармен жұмыс істеу; 2. үлкен топ оқушылармен сабақ; 3. оқушылардың тұрақты құрамы, жасы және даму деңгейі шамамен бірдей, мұғалімдердің оқушылар тобымен ұжымдық формамен жұмыс істеу; 4. белгілі жобалар бойынша оқушылармен жұмыс істеу; 5. оқушылардың жеке жұмысы 49. ХХ ғ. басындағы Германиядағы Георг Кершенштейнердің педагогикалық теориясының негізгі идеясы: 1. дамытушылық оқыту; 2. элементарлық білім беру; 3. азаматтық тәрбие; 4. табиғи тәрбие; 5. мәдениетке сай тәрбие 50. Кершенштейнердің ойынша азаматтық тәрбие балаларды үйретуге тиісті: 1. азамат болуға; 2. мемлекетке бағынуға; 3. христиандік тілалғыштыққа; 4. әлемнің адамы болуға; 5. отбасыны құндылауға 51. Прагматикалық педагогиканың негізгі идеялары: 1. басқару аппаратты тәрбиелеу; 2. мектепті өмірмен байланыстыру, іскер адамды тәрбиелеу; 3. тағдыр мен жағдайға көнетін тұлғаны тәрбиелеу; 4. діншіл адамды тәрбиелеу; 5. еркін адамды тәбиелеу 52. Монтессоридің “сенсорлық тәрбиесінің” негізін құрайтың келесі педагогтың идеясы: 1. Дьюи; 2. 1Песталоцци; 3. Дистервег; 4. Коменский; 5. Руссо 53. М. Монтессоридің пікірінше, тәрбиенің негізгі міндеті: 1. жан-жақты үйлесімді дамыған тұлғаны қалыптастыру; 2. нағыз азаматты тәрбиелеу; 3. балалардың табиғи бейімділігіне дамытатын ортаны құрастыру; 4. әлеуметтік тәжірибені және өмірге дайындықты балаларға тапсыру; 5. өмірге деген қызығушылықты қалыптастыру 54. “Мұғалім мамандығы – күн астындағы ең қадірлі мамандық” – деген:
|

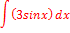
 ; г)0.
; г)0.

 г)
г)  .
.
 +с; в)2x2
+с; в)2x2  .
.
 +с; в)
+с; в)  ; г)
; г)  .
.
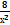 +с; в)
+с; в)  ; г)
; г)  .
.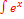 dx
dx ; г)
; г)  ; б)20
; б)20  ; в)1
; в)1  ; г)4.
; г)4. ; б)
; б)  ; в) -
; в) -  ; г)4
; г)4  .
. .
. ; б) 2
; б) 2  ;г)- 2
;г)- 2  ; в)6
; в)6  ;г) 3.
;г) 3. ; б)4
; б)4  ; в)1
; в)1  ; г)2
; г)2  .
. ; в)
; в)  .
.
 ; г) -2.
; г) -2.
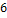 ; г)11.
; г)11.
 ; в)
; в) 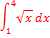
 ; в)
; в)  ; г)
; г) 

 ; г)2
; г)2

 ; г)-4
; г)-4 ,
,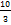 ; в)
; в)  ; г)5
; г)5
 ; б) 10; в)18; г)
; б) 10; в)18; г) 
 ; в)e; г)8ln4 – 4 -
; в)e; г)8ln4 – 4 -  .
. ,
, ,
, ; в) -
; в) -  .
. .
. ,
, ; б)
; б) 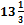 .
. ,
, .
. ; б)
; б)  ; в)1; г) 0.
; в)1; г) 0. ,
, ; б)
; б)  ; в)1; г)
; в)1; г)  .
.
 ; г)
; г)  .
.
 ; б)
; б)  ; в)
; в)  ; г)
; г) 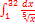 ,
, ; в)
; в)  .
.
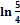 ; б)
; б)  ; в)tg
; в)tg  ; г)
; г)  ,
, ; в) - 1; г)
; в) - 1; г)  .
. ,
, ; б)
; б)  ; в)
; в)  ; г)
; г)  ,
,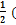 е – 1);в) е
е – 1);в) е 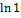 ; г)
; г)  .
. .
. -3
-3  ;б)2
;б)2  ; в)8
; в)8  .
.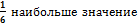 ;
; ;
; ;
; 22.
22.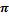 ; б)81
; б)81  ; в)18
; в)18 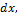 зная,что при х=2 функция принимает значение, равное 20.
зная,что при х=2 функция принимает значение, равное 20. - 2x+14; в)y = 10x– 2; г)y = 5x-2
- 2x+14; в)y = 10x– 2; г)y = 5x-2 .
. +c; б)10
+c; б)10  ; в)
; в) 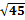 ; г)
; г)  .
. ; б) v =36
; б) v =36  ;
;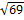 .
. .
. .
. .
. .
. .
. .
. ; б) 4; в)
; б) 4; в)  г)27.
г)27. ; б)17; в)22; г) 18.
; б)17; в)22; г) 18.


