Оптимизация режима работы дуговой сталеплавильной печи
Эффективное управление современными дуговыми сталеплавильными печами (ДСП), оснащенными водоохлаждаемыми панелями на стенках и своде печи, представляет собой довольно не простую задачу. Дополнительную сложность вносит корректировка суточных графиков нагрузки, поэтому требуется разработка методов расчета оптимального режима работы. Особенно это необходимо для периода плавки, когда в печи образуется ванна жидкого металла, так как при непосредственном излучении дуги на стены и свод печи влияние водоохлаждаемых панелей на энергетический режим ДСП максимально и изменение параметров плавки существенно отражается на качестве продукции. С целью оптимизировать энергетический режим работы ДСП в период образования жидкой ванны определяют значения и моменты переключения ступеней напряжения печного трансформатора и уставок тока, т.е. решают задачу оптимального управления [8]. Использовались два критерия оптимальности – время и расход энергии при нагреве жидкого металла до заданной температуры. Первый критерий характерен для современных ДСП, предназначенных для выпуска максимального количества жидкого полупродукта, доводка которого до заданного состава производится в устройствах внепечной обработки стали, второй позволяет обеспечить в рассматриваемый период минимальные энергетические затраты. Математически задачи оптимизации можно сформулировать следующим образом: для первого критерия: найти такие функции U(τ), I(τ), чтобы условие Tм(τ*) = Тм.з. выполнялось при минимальном значении τ* (0 ≤ τ ≤ τ*); для второго критерия: найти функции U(τ), I(τ), обеспечивающие минимум W= Здесь U(τ), I(τ) – действующие значения фазных напряжений и токов Тм(τ) – температура жидкого металла; Тм.з –заданная температура, до которой необходимо нагреть металл; P (U,I,τ) – подводимая электрическая мощность; W – полная энергия. При расчете оптимальных режимов нагрева металла необходимо учесть ограничения на токи, напряжения и на тепловые нагрузки в рабочем пространстве печи. В целях сокращения размерности решаемой задачи с учетом, что отклонения от симметричных режимов в современных печах относительно невелики, принято допущение о симметрии трехфазной электрической цепи ДСП. В этом случае U(τ) = U1(τ) = U2(τ) = U3(τ); I(τ) = I1(τ) = I2(τ) = I3(τ) и ограничения на электрические параметры имеют вид: Umin≤ U(τ) ≤ Umax , (3.10) 0 ≤ I(τ) ≤ I(τ) ≤ Imax, (3.12) Uд(τ) ≤ а U(τ). (3.13) Ограничение (4.10) на значение фазного напряжения U определяется диапазоном переключения ступеней напряжений (приведенных к фазным) с вторичной стороны печного трансформатора от минимального Umin до максимального Umax. Ограничение (3.11) характеризует максимально допустимую мощность трансформатора S при работе на ступени, соответствующей напряжению U, (3.12) связано с максимально допустимой плотностью тока, (3.13) отражает условия непрерывного горения дуг. При этом коэффициент а = 0,82 Uд (τ) = I(τ) [ где r и x – активное и реактивное сопротивление подводящей цепи ДСП. Ограничения на тепловые нагрузки в рабочем пространстве печи включают в себя ограничения на температуру внутренней поверхности футерованных стен и свода Tст ≤ Тф; Тсв ≤ Тф , (3.15) и на удельный тепловой поток, приходящийся на водоохлаждаемые панели qст ≤ qв; qсв ≤ qв, (3.16) где Тф – максимально допустимая температура футеровки; qст, qсв – удельные тепловые потоки на водоохлаждаемые панели стен и свода; qв – поток, максимально допустимый для данной конструкции водоохлаждаемых панелей. Вычисление критериев оптимизации и ограничений основывается на разработанной ранее математической модели теплообмена в рабочем пространстве дуговой печи в период жидкой ванны [10]. При разработке модели учитывались следующие механизмы теплообмена: теплообмен излучением между дугами, поверхностью шлака, электродами, внутренней поверхностью стен и свода. Сформулированные задачи оптимального управления энергетическим режимом дуговых печей характеризуются сложными ограничениями на управление I(τ), U(τ) (1) – (3.13) и тепловыми нагрузками в рабочем пространстве печи (3.15), (3.16). Кроме того, уравнения динамики процесса, включающие в себя уравнения в частных производных, обыкновенное дифференциальное уравнение и алгебраические уравнения – не линейны. Численное решение этой весьма сложной задачи основывалось на дискретизации по пространственным переменным и замене уравнений в частных производных обыкновенными дифференциальными уравнениями, а также на кусочно-постоянной аппроксимации функций I(τ), U(τ). Разработанное математическое обеспечение было использовано для расчета оптимальных режимов нагрева металла в дуговой сталеплавильной печи ДСП-30. Рассматривается режим нагрева 30т металла с 1500 до 1700 0С при ограничениях на тепловые нагрузки: Tф=1670 0С, qв = 300 кВт/м2. Расчеты, проведенные при различном числе переключений токов и напряжений, показатели, что увеличение числа интервалов слабо влияет на целевую функцию и двух интервалов вполне достаточно для практической реализации оптимального режима. В табл. 3.4 приведены результаты расчета режимов наискорейшего нагрева при hш = 10 см (толщине шлака) и двух интервалах постоянства токов и напряжений.
Таблица 3.4 – Параметры режима нагрева
Оптимальный режим имеет два характерных участка: на первом происходит интенсивный нагрев металла, не лимитированный тепловыми ограничениями, а на втором вводимая мощность ограничивается температурой футеровки и выбирается из условия ее поддержания на максимально допустимом уровне. Разработанный оптимальный электротехнологический режим позволяет достигать необходимую температуру при минимальном времени нагрева жидкого металла с минимальным числом переключений ступеней напряжения печного трансформатора. Таким образом, достигается наибольшая производительность при минимизации амортизационных издержек.
|

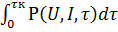 при выполнении условия I(τк)= Тм.з.
при выполнении условия I(τк)= Тм.з. , (3.11)
, (3.11) 0,9 и зависит от соотношения активного и реактивного сопротивления подводящей цепи ДСП, действующее напряжение на дуге Uд вычисляется по формуле [9]:
0,9 и зависит от соотношения активного и реактивного сопротивления подводящей цепи ДСП, действующее напряжение на дуге Uд вычисляется по формуле [9]: ], (3.14)
], (3.14)


