Аннотация.Опредеделения ряда динамики. Показатели ряда динамики. Анализ ряда динамики.
Динамический ряд представляет собой хронологическую последовательность числовых значений статистических показателей. Виды рядов динамики (РД): 1) моментные (моментальные) РД; 2) интервальные РД; 3) РД с нарастающими итогами; 4) производные РД. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Пример моментного ряда динамики:
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Каждый уровень интервального ряда складывается из данных за более короткие интервалы. Пример интервального ряда динамики:
Производные ряды – ряды, уровни которых представляют собой не непосредственно наблюдаемые значения, а производные величины: средние или относительные. Основные направления изучения закономерностей развития социально-экономических явлений с помощью рядов динамики: - характеристика уровней развития изучаемых явлений во времени; - измерение динамики изучаемых явлений посредством системы статистических показателей; - выявление и количественная оценка основной тенденции развития (тренда); - изучение периодических колебаний; - экстраполяция и прогнозирование. Таблица 1 Уровни (показатели) ряда динамики
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней. Средний уровень интервального ряда определяется по формуле средней арифметической простой:
где n – число уровней. В моментном ряду динамики с равностоящими датами средний уровень определяется по формуле средней хронологической простой:
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней хронологической взвешенной:
где уi – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti. Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
|

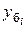 = yi – у 0 (6.1)
= yi – у 0 (6.1)
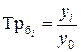 (6.2)
(6.2)
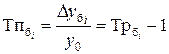 (6.3)
(6.3)
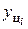 = yi – yi -1 (6.4)
= yi – yi -1 (6.4)
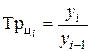 (6.5)
(6.5)
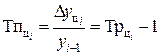 (6.6)
(6.6)
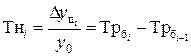 (6.7)
(6.7)
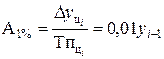 (6.8)
(6.8)
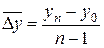 =
= 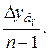 (6.9)
(6.9)
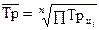
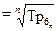
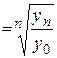 (6.10)
(6.10)
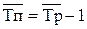 (6.11)
(6.11)
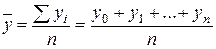 , (6.12)
, (6.12)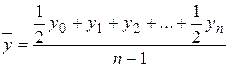 .(6.13)
.(6.13)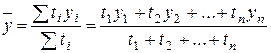 ,(6.14)
,(6.14)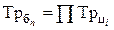 ;
; 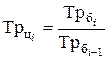 .(6.15)
.(6.15)


