Общие индексы качественных показателей
1.Индексы цен показывают, как изменилась стоимость продукции за счет изменения цен. Агрегатный индекс цен Пааше:
где p 1 q 1 – фактическая стоимость продаж (товарооборот) в отчетном периоде; p 0 q 1 – условная стоимость товаров, реализованных в отчетном периоде по базисным ценам. 2. Агрегатный индекс цен Ласпейреса:
где p 0 q 0 – фактическая стоимость продаж (товарооборот) в базисном периоде; p 1 q 0 – условная стоимость товаров, реализованных в базисном периоде по отчетным ценам. Индекс цен Пааше показывает изменение цен отчетного периода по сравнению с базисным (на сколько товары стали дороже (дешевле)). Если бы товары были реализованы в отчетном периоде по базисным ценам, то фактическая экономия составила
Индекс цен Ласпейреса показывает условную экономию, т.е. на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде. Этот индекс применяется при прогнозировании объема товарооборота в связи с предлагаемым изменением цен. В условиях стабильности применяют индекс Пааше, при инфляции – индекс Ласпейреса. Основываясь на рассмотренных двух вариантах построения индексов, Фишер предложил рассчитывать среднюю геометрическую индексов цен Пааше и Ласпейреса:
Этот индекс носит название “ идеальный ” индекс цен Фишера. Индекс цен Фишера “обратим” во времени (т.е. если рассчитывать индекс базисного периода к отчетному, он будет равен обратной величине первоначального индекса), но лишен экономического содержания. При синтезировании общего индекса цен вместо фактического количества товаров (в отчетный и базисный периоды) в качестве соизмерителей индексируемых величин р 1 и р 0 могут применяться средние величины реализации товаров. При таком способе расчета формула сводного индекса цен (называемого индексом цен Лоу) выглядит следующим образом:
Индекс цен Лоу применяется в расчетах при закупках или реализации товаров в течение продолжительных периодов времени (пятилетках, десятилетиях и т.п.), поскольку он дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров. Пример 2. По имеющимся данным о ценах и реализации неоднородных товаров за два периода необходимо определить индексы цен: 1) индивидуальные; 2) агрегатные, в т.ч. а) индекс Пааше; б) индекс Ласпейреса; в) “идеальный” индекс Фишера; г) индекс Лоу.
Сведем расчет индивидуальных индексов цен и промежуточные расчеты для определения агрегатных индексов цен в таблицу:
а) Индекс цен Пааше
Абсолютный прирост товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом составил
т.е. если бы уровень цен остался на уровне базисного периода, экономия потребителя составила бы 40000 руб. б) Индекс цен Ласпейреса
Абсолютный прирост товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом составил
в) “Идеальный” индекс цен Фишера
г) Индекс цен Лоу
|

 , (7.8)
, (7.8) , (7.9)
, (7.9)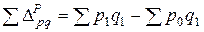 . (7.10)
. (7.10) . (7.11)
. (7.11)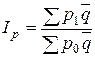 . (7.12)
. (7.12)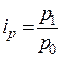
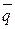
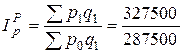 = 1,1391 (113,91%).
= 1,1391 (113,91%).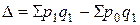 = 327500 – 287500 = 40000 руб.,
= 327500 – 287500 = 40000 руб.,
 = 1,1444 (114,44%).
= 1,1444 (114,44%). = 257500 – 225000 = 32500 руб.
= 257500 – 225000 = 32500 руб.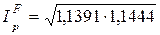 =1,1418 (114,18%).
=1,1418 (114,18%). = 1,1415 (114,15%).
= 1,1415 (114,15%).


