Задача 1. Имеются следующие данные о распределении рабочих предприятия по квалификации (тарифному разряду): Группа рабочих предприятия по тарифному разряду
Имеются следующие данные о распределении рабочих предприятия по квалификации (тарифному разряду):
На основании имеющихся данных определите по цехам предприятия и по предприятию в целом: 1) средний тарифный разряд рабочих; 2) модальные и медианные значения тарифного разряда рабочих. Поясните экономическое содержание этих показателей; 3) абсолютные показатели вариации тарифного разряда рабочих; 4) относительные показатели вариации тарифного разряда рабочих. Сравните вариацию тарифного разряда рабочих по цехам предприятия и по предприятию в целом. Решение. Для удобства дальнейших вычислений составляем таблицу.
Таблица 11.1. -Промежуточные вычисления для расчета показателей вариации.
1. Средний тарифный разряд работников по каждому цеху и по всему предприятию определим по формуле средней арифметической взвешенной. По первому цеху:
По второму цеху:
По всему предприятию в целом:
Найдем моду Мо, исходя из того, что модальному значению соответствует разряд имеющий наибольшую частоту. Для первого цеха: Мо(1) = 4 разряд. Наибольшее число работников 1-го цеха имеют 4-ый разряд. Для второго цеха: Мо(2) = 4 разряд. Наибольшее число работников 2-го цеха имеют 4-ый разряд. По всему предприятию в целом: Мо= 4 разряд. Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда: NMe = (n + 1)/2, где n – объем совокупности. Медиана – это варианта, располагающаяся в середине ранжированного ряда распределения. Для первого цеха: NMe(1) = (100 + 1)/2 = 50,5 Точная середина располагается между 50-м и 51-м работником. Данные работники имеют 4-ый разряд, следовательно Ме(1) = 4 разряд. Половина работников 1-го цеха имеют разряд до 4, а вторя половина работников имеет разряд более 4. Для второго цеха: NMe(1) = (200 + 1)/2 = 100,5 Точная середина располагается между 100-м и 101-м работником. Данные работники имеют 4-ый разряд, следовательно Ме(2) = 4 разряд. Половина работников 2-го цеха имеют разряд до 4, а вторя половина работников имеет разряд более 4. По всему предприятию в целом: NMe(1) = (300 + 1)/2 = 150,5 Точная середина располагается между 150-м и 151-м работником. Данные работники имеют 4-ый разряд, следовательно Ме = 4 разряд. Половина работников предприятия имеют разряд до 4, а вторя половина работников имеет разряд более 4. К абсолютным показателям вариации относятся дисперсия и среднее квадратическое отклонение. Найдем дисперсию по следующей формуле:
Среднее квадратическое отклонение находим формуле:
Размах вариации: R = Xmax – Xmin = 8 – 7 = 7 разряд. Среднее линейное отклонение:
Для первого цеха:
s1 = 1,476 разряд. Разброс наблюдений относительно средней величины составляет 1,476 тарифных единиц. Среднее линейное отклонение: d1= 118,4/100 = 1,184 разряда. Для первого цеха:
s2 = 1,498 разряд. Разброс наблюдений относительно средней величины составляет 1,498 тарифных единиц. Среднее линейное отклонение: d2= 239,44/200 = 1,2 разряда. Для всего предприятия:
s = 1,491 разряд. Разброс наблюдений относительно средней величины составляет 1,491 тарифного разряда. Среднее линейное отклонение: d= 358,2/300 = 1,19 разряда. 2. К относительным показателям вариации относится коэффициент вариации. Коэффициент вариации определим по формуле:
Коэффициент осцилляции:
Линейный коэффициент вариации:
Для 1-го цеха: V1 = 1,476/4,4 = 0,336 или 33,6%. VR1 = 7/4,4 = 1,591 или 159,1 %. Vd1 = 1,18/4,4 = 0,269 или 26,9%. Для 2-го цеха: V2 = 1,498/4,31 = 0,348 или 34,8%. VR2 = 7/4,31 = 1,624 или 162,4 %. Vd2 = 1,2/4,31 = 0,278 или 27,8%. Для всего предприятия: V = 1,491/4,34 = 0,344 или 34,4%. VR = 7/4,34 = 1,613 или 161,3 %. Vd = 1,19/4,34 = 0,275 или 27,5%. Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние характеристики достаточно надежно характеризуют совокупность по варьирующему признаку. В нашем же случае, коэффициент вариации не больше 35%, как для цехов в отдельности, так и для всего предприятия в целом. Следовательно, полученная средняя величина тарифного разряда ненадежно характеризует данную совокупность по этому признаку. По относительным показателям вариации между показателями каждого из цехов и всех цехов вместе практически нет различий. Т. е. показатели вариации по тарифному разряду в каждом цехе практически одинаковые.
|




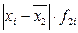


 4,4 разряд.
4,4 разряд. 862/200 = 4,31 разряд.
862/200 = 4,31 разряд. 1302/300 = 4,34 разряд.
1302/300 = 4,34 разряд. .
.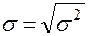 .
.
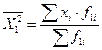 = 2154/100 = 21,54 разряд2
= 2154/100 = 21,54 разряд2 21,54 – 4,42 = 2,18 разряд2
21,54 – 4,42 = 2,18 разряд2 = 4162/200 = 20,82 разряд
= 4162/200 = 20,82 разряд 20,82 – 4,312 = 2,244 разряд
20,82 – 4,312 = 2,244 разряд = 6318/300 = 21,06 разряд
= 6318/300 = 21,06 разряд 21,06 – 4,342 = 2,224 разряд
21,06 – 4,342 = 2,224 разряд .
.




