Задача 7. Распределение малых предприятий региона по стоимости основных производственных фондов (ОПФ) за год составило
Распределение малых предприятий региона по стоимости основных производственных фондов (ОПФ) за год составило, млрд р. (см.таблицу ниже).
В таблице: а - вариант, соответствующий наибольшей частоте. При ƒ=10, а =19; k = 20 – 18 = 2. Вычисляем момент первого порядка: х – а ∑------ƒ k 17 m 1 = ------------- = ---- = 0,34; ∑ƒ 50 _ х = km 1 + a = 2 * 0,34 + 19 = 19,68 млрд р. Мода и медиана при расчете не связаны с какой-то общей характеристикой, а представляют собой конкретный вариант в соответствии с их сущностью. Мода - значение признака (варианта), который чаще всего встречается в совокупности. Медиана - значение признака в середине ряда. Расчет моды и медианы зависит от вида ряда - дискретного или интервального. По дискретному ряду их находят без формул, по определению, визуально. Мода - по наибольшей частоте, медиана соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером n + 1 NMe =-------, где n - число единиц в совокупности. По накопленным частотам определяют ее численное значение в дискретном вариационном ряду; по интервальному - по следующим формулам: а) мода: ƒ1 – ƒ2 M0 = x0 + k -------------------------, (ƒ2 – ƒ1) + (ƒ2 – ƒ3) где ƒ2 - наибольшая (модальная) частота интервала; ƒ1 – частота интервала, стоящая перед, модальным; ƒ3 - частота интервала, последующего за модальным; х0 - канальное значение модального интервала; k - размер модального интервала. (Модальный интервал находится по наибольшей частоте); б) медиана: n + 1 ------ - Sm – 1 Me = x0 + k -------------------, fm где fm - частота медианного интервала; п - сумма всех частот ряда; Sm - 1 - сумма накопленных частот до интервала, содержащего медиану; х0 - начальное значение медианного интервала; k — размер медианного интервала. n +1 Место медианы определяется по формуле Nme = ------. По данным предыдущего примера найдем моду и медиану.
ƒ1 – ƒ2 16 – 9 M0 = x0 + k -------------------------= 18 + 2 ------------------------ = 18 + 2*0,64 = (ƒ2 – ƒ1) + (ƒ2 – ƒ3) (16 – 9) + (16 – 12)
= 18 + 1,28 = 19,28 млрд р. Модальным значением стоимости ОПФ малых предприятий региона является стоимость, равная 19,28 млрд р. Для дискретного ряда М0 = 19 млрд р. (по наибольшей частоте ƒ = 16). n + 1 50 + 1 Место медианы Nme = ------ = -------- = 25,5; 2 2 следовательно, медиана для дискретного ряда равна 19 млрд р. Медианным является интервал 18 – 20 млрд р., так как в этом интервале находятся номера 25 и 26. Найдем медианный интервал, для чего произведем накопление частот; (3 + 9 + 16) = 28, что превышает половину суммы всех частот (50: 2 = 25). Начальное значение медианного интервала - 18, его частота - 16, сумма накопленных частот до него - 12. n + 1 ------ - Sm – 1 2 25,5 – 12 Me = x0 + k ------------------ = 18 + 2 -------------- = 18 + 2 * 0,84375 = fMe 16
= 18 + 1,6875 = 19,6875 млрд р. Это означает, что из 50 малых предприятий региона 25 имеют стоимость ОПФ менее 19,6875 млрд р., а 25 предприятий - более. Квартиль - значение признака, делящее ранжированную совокупность на 4 равные по численности части. Различают нижний квартиль Q1, отделяющий ¼часть совокупности с наименьшими значениями признака, и квартиль верхний Q3, отделяющий ¾ части совокупности с наибольшими значениями признака. Это значит, что 25% единиц совокупности будут меньше по величине Q1;25% единиц будут заключены между Q1 и Q2; 25% единиц будут заключены между О2 и Q3 и 25% превосходят Q3. Второй квартиль является медианой (средний квартиль). Вычисление квартилей аналогично вычислению медианы. Сначала определяют положение или место квартиля: n + 1 n + 1 n + 1 n + 1 NQ1 = -------; NQ2 = ------- * 2 = -------; NQ3 = ------- * 3. 4 4 2 4 Затем по накопленным частотам в дискретном ряду определяют численное значение. В интервальном ряду распределения в начале указывают интервал, в котором находится квартиль, затем определяют его численное значение по формуле: NQ – SQ – 1 Q = XQ + k -------------, fQ где XQ - нижняя граница интервала, в котором находится квартиль; SQ – 1 накопленная частота интервала, предшествующая тому, в котором находится квартиль; fQ - частота интервала, в котором находится квартиль. Продолжим решение задачи 5 распределения малых предприятий по стоимости основных производственных фондов (ОПФ) за год. В таблице представлено распределение предприятий по стоимости ОПФ и необходимо определить квартили.
Производим накопление частот в % к итогу числа предприятий (табл. 4.3). Определяем положение или место, в котором находится квартиль по накопленным частотам: n + 1 50 + 1 n + 1 50 + 1 NQ1 = ------- = -------- = 12,75; NQ3 = ------- * 3 = -------- * 3 = 38,25. 4 4 4 4 Интервал, в котором находится квартиль: нижний – 18 – 20 с накопленной частотой 56 %; верхний – 20 – 22 с накопленной частотой 80%. Нижний квартиль вычисляется по формуле: NQ – SQ1 – 1 12,75 - 12 Q1 = XQ1 + k -------------- = 18 + -------------- = 18 + 0,047 = 18,047 ≈ 18 млрд р. fQ1 16 n + 1 ------- * 3 – SQ3 – 1 4 38,75 - 28 Верхний квартиль: Q3 = XQ3 + k ----------------------- = 20 + -------------- = fQ3 12 = 20 + 0,896 = 20,896 ≈ 21 млрд р. Следовательно, 25 % предприятий имеют стоимость ОПФ менее 18 млрд р. 25 % - свыше 21 млрд р. а остальные предприятия имеют доход в пределах от 18 до 21 млрд р. по стоимости ОПФ. Пример:Имеются выборочные данные о стаже работников коммерческих банков (см.таблицу ниже).Определить показатели вариации. Стаж работы и численность работников коммерческих банков
Находим средний стаж работников по формуле методом моментов:
где а = 4 при наибольшей частоте f = 48, k = (5 – 3) = 2. Момент первого порядка:
1. Размах вариации: R = х max - x min = 10 – 2 = 8 лет. 2. Среднее линейное отклонение: 3. Дисперсия по способу моментов:
4. Среднее квадратическое отклонение: 5. Коэффициент осцилляции 6. Относительное линейное отклонение 7. Коэффициент вариации Можно вычислить в данном примере среднюю величину и дисперсию обычным способом по сгруппированным данным для дискретного ряда распределения: а) средний стаж работников: б) средний квадрат (дисперсия): в) кроме того, дисперсию можно вычислить по упрощенной формуле:
для сгруппированных данных:
Получается одно и то же значение дисперсии независимо от применяемой формулы вычисления. Задача 8. (на правило сложения дисперсий). При изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда в цехе были получены данные, представленные в таблице. Определить общую и групповую дисперсию и среднюю из внутригрупповых дисперсий, проверить правило сложения дисперсий; коэффициент детерминации; эмпирическое корреляционное отношение. . Распределение рабочих по среднечасовой выработке изделий
В примере данные группируются по квалификации (тарифному разряду) рабочих, являющейся факторным признаком х. Результативный признак уi, варьирует как под влиянием систематического фактора х - квалификации, так и других неучтенных случайных факторов (внутригрупповая вариация). Необходимо измерить эту вариацию с помощью дисперсий. 1. Вначале вычислим средние выработки по каждой группе и общую среднюю по формуле средней арифметической простои Вычисление внутригрупповых дисперсий проводится по формулам простым по каждой группе: первая Внутригрупповые дисперсии показывают вариации выработки в каждой группе, вызванные всеми возможными факторами, кроме различий в квалификационном разряде, так как внутри группы все рабочие имеют одну квалификацию. 2. Средняя из внутригрупповых дисперсий
Эта дисперсия отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих в среднем по всей совокупности. 3. Исчислим межгрупповую дисперсию по формуле:
Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификации. 4. Исчислим общую дисперсию по формуле:
Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию среднечасовой выработки изделий всеми рабочими цеха. 5. Правило сложения дисперсий:
6. Коэффициент детерминации:
Следовательно, на 66,67% вариация производительности труда рабочих вызвана различиями в их квалификации и на (100 - 66,67) = 33,33% - влиянием всех прочих неучтенных случайных факторов. 7. Эмпирическое корреляционное отношение:
что свидетельствует о тесной связи между квалификацией рабочих и производительностью их труда.
|







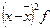

 ;
; лет - средний стаж работников.
лет - средний стаж работников.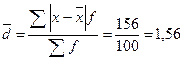 лет.
лет.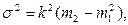
 т.е.
т.е. 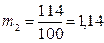 - момент второго порядка;
- момент второго порядка;
 г. Стаж работников банка отклоняется от среднего стажа 5 лет на 1,9 гоа в ту и другую сторону.
г. Стаж работников банка отклоняется от среднего стажа 5 лет на 1,9 гоа в ту и другую сторону. ; разница между крайними значениями по стажу работы составляет 160% среднего значения.
; разница между крайними значениями по стажу работы составляет 160% среднего значения.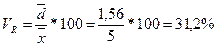 ; абсолютное отклонение от средней величины составляет 31,2 %.
; абсолютное отклонение от средней величины составляет 31,2 %. , так как V>33%;следовательно, выборочное наблюдение о стаже работников коммерческих банков не является однородным, и для дальнейшего анализа нужно пересмотреть исходный ряд распределения. Данный ряд нельзя использовать в целях прогноза.
, так как V>33%;следовательно, выборочное наблюдение о стаже работников коммерческих банков не является однородным, и для дальнейшего анализа нужно пересмотреть исходный ряд распределения. Данный ряд нельзя использовать в целях прогноза. лет;
лет; ;
;




 . По первой группе
. По первой группе  по второй группе
по второй группе  ; по двум группам вместе:
; по двум группам вместе: 
 ; вторая
; вторая 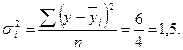




 или 66,67%.
или 66,67%.



