| Тема 7
| МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
‒ процессы в механических системах, в которых периодически изменяются координата, скорость, ускорение и сила
| |
| ● примеры
механических
колебаний
| ➨движение часового маятника; обращение Земли вокруг Солнца; колебание струны; излучение и передача звука;
| |
| АМПЛИТУДА
колебания
А [м]
| ➨максимальное смещение колеблющейся точки от положения равновесия;
| |
ПЕРИОД колебаний
Т=  [с] [с]
| ➨время одного полного колебания;
➨ t -время колебаний;
➨ n- число колебаний;
| |
● частота колебаний
 или или  [Гц = с-1] [Гц = с-1]
| ➨число полных колебаний, совершенных в единицу времени;
| |
| ● единица частоты
1 Герц
| ➨частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание;
| |
| ГАРМОНИЧЕСКИЕ
КОЛЕБАНИЯ
| ➨простейшие периодические колебания, при которых координата тела хменяется со временем по закону синуса  или косинуса или косинуса  ; ;
| |
| ● пример
гармонического
колебания
| ➨движение точки Мпо окружности радиуса А с постоянной угловой скоростью  ; ;
| 
| |


| ➨ координаты точки М
 для угла для угла  ; ;
| |
 , , 
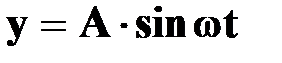 , , 
| ➨если точкаМ движется по окружности с постоянной угловой скоростью  , то координаты точки изменяются по гармоническим законам; , то координаты точки изменяются по гармоническим законам;
| |


| ➨если точка Мповернулась на угол  (в момент времени (в момент времени  ), то необходимо внести поправку в уравнения движения; ), то необходимо внести поправку в уравнения движения;
| |
| ФАЗА колебания
φ= (ωt+φ0) [рад]
| ➨величина, стоящая под знаком sin или cos,и пока-зывающая, какая часть периода прошла от момента начала колебания;
| |
ПЕРИОД
гармонических
колебаний
 [с] [с]
| ➨промежуток времени, в течение которого фаза колебания получает приращение  ; ;
| |
ЦИКЛИЧЕСКАЯ
(круговая) ЧАСТОТА
 или или  [рад/с] [рад/с]
| ➨число колебаний, совершаемых за время  с; с;
| |
| ● графическое
представление
гармонических
колебаний
|  ➨ ➨
| |
| СКОРОСТЬ
колеблющейся точки
| ➨ 
| |
| УСКОРЕНИЕ
колеблющейся точки
| ➨ 
| |
| Свободные
(собственные)
колебания
| ➨колебания, которые совершает система (тело) после того, как она была выведена из состояния устойчивого равновесия и затем предоставлена самой себе.
➨ при наличии сил трения свободные колебания будут затухающими.
| |
| Затухающие
колебания
| ➨колебания, амплитуда которых уменьшается с течением времени (за счет действия сил трения и других сил сопротивления);
| 
|
| ОСЦИЛЛЯТОР
| ➨любая физическая система, совершающая колебания
Классические осцилляторы:
● физический маятник,
● математический маятник;
● пружинный маятник;
| |
| ФИЗИЧЕСКИЙ
маятник
| ➨твердое тело произвольной формы, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести;
| 
| |
| | |
| МАТЕМАТИЧЕСКИЙ маятник
| ➨идеализированная система, состоящая из материальной точки массой m,подвешенной на нерастяжимой невесомой нити длиной  , и колеблющейся под действием силы тяжести (если предположить, что вся масса физического маятника сосредоточена в одной точке - центре масс, то математический маятник - частный случай физического маятника); , и колеблющейся под действием силы тяжести (если предположить, что вся масса физического маятника сосредоточена в одной точке - центре масс, то математический маятник - частный случай физического маятника);
| 
| |
| | |
| Ускорение
| ➨   ;при малых углах ;при малых углах  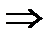  ;
➨знак «-» учитывает противоположное направление векторов смещения ;
➨знак «-» учитывает противоположное направление векторов смещения  и силы и силы  ; ;
| |
| Период
собственных
колебаний
| ➨ 
| |
Частота собственных колебаний

| Циклическая (круговая) частота
 или или 
| |
| ПРУЖИННЫЙ
маятник
| ➨груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы Fупр= - kx (k- жесткость пружины).
Знак «-» учитывает противоположное направление векторов смещения и силы упругости  . .
| |

| |
| Ускорение
| ➨ 
| |
| Период
собственных
колебаний
| ➨ 
| |
Частота собственных колебаний

| Циклическая (круговая) частота
 или или 
| |
| ПРЕВРАЩЕНИЕ
ЭНЕРГИИ
при гармонических колебаниях
| ➨при всяком колебании происходит переход потенциальной энергии 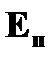 в кинетическую в кинетическую 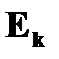 и наоборот.
При максимальном отклонении маятника от положения равновесия его скорость и наоборот.
При максимальном отклонении маятника от положения равновесия его скорость  и кинетическая энергия и кинетическая энергия  , а , а 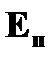 имеет максимальное значение. Проходя положение равновесия, маятник имеет максимальную скорость, следовательно максимальную имеет максимальное значение. Проходя положение равновесия, маятник имеет максимальную скорость, следовательно максимальную 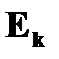 и нулевую потенциальную энергию: и нулевую потенциальную энергию:  . .
| |
| КИНЕТИЧЕСКАЯ
энергия
| ➨ 
| |
| ПОТЕНЦИАЛЬНАЯ
энергия
| ➨ 
| 

|  
| |

| |
| ПОЛНАЯ
энергия
| ➨ 
| |
| ВЫНУЖДЕННЫЕ
КОЛЕБАНИЯ
| ➨колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы, называемой вынуждающей силой;
| |
Резонанс

 = = 
| ➨явление резкого возрастанияамплитуды вынужденных колебанийпри совпадении частоты  периодического внешнего воздействия с частотой периодического внешнего воздействия с частотой  собственных колебаний осциллятора;
➨ возрастание амплитуды тем больше, чем меньше трение в системе; при малом трении резонанс «острый» (кривая 1), при большом трении – «тупой» (кривая 2); собственных колебаний осциллятора;
➨ возрастание амплитуды тем больше, чем меньше трение в системе; при малом трении резонанс «острый» (кривая 1), при большом трении – «тупой» (кривая 2);
| |
| Амплитуда
вынужденных
колебаний
при резонансе
| 
|  -амплитудное значение внешней силы; -амплитудное значение внешней силы;
 -коэффициент трения. -коэффициент трения.
| |
| АВТОКОЛЕБАНИЯ
| ➨незатухающие колебания в системе поддерживаемые внешними источниками энергии при отсутствии воздействия внешней переменной силы;
| |
| · отличие от
вынужденных
колебаний
| ➨частота и амплитуда автоколебаний определяются свойствами самой колебательной системы;
| |
| · отличие от
свободных
колебаний
| ➨автоколебания отличаются независимостью амплитуды от времени и от начального кратковременного воздействия, возбуждающего процесс колебаний;
| |
| · основные элементы
автоколебательной
системы
| ➨

| |
| ● источник энергии
| ➨ компенсирует потери энергии на затухание колебаний за счет трения или других сил сопротивления; энергия, поступающая из источника за период, равна энергии, потерянной в колебательной системе за то же время;
| |
| ● осциллятор
| ➨колебательная система;
| |
| ● клапан
| ➨устройство, которое регулирует поступление энергии в колебательную систему;
| |
| ● обратная связь
| ➨устройство для обратного воздействия автоколебательной системы на клапан, управления работой клапана за счет процессов в самой колебательной системе;
| |
| · пример
автоколебательной
системы
| ➨часы; паровые машины и двигатели внутреннего сгорания; отбойные молотки; электрические звонки.
| |
| · часы с маятником
| ➨ колебательной системой является маятник, источником энергии – гиря, поднятая над землей (или стальная пружина); устройства обратной связи – ходовое колесо и анкер.
Гиря (или пружина) вызывает вращение ходового колеса. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в таком направлении, что разгоняет маятник.
В результате запас энергии, израсходованной на трение, восполняется за счет энергии гири, поднятой над землей (или закрученной пружины). Вращение стрелок часов осуществляется с помощью зубчатых колес от ходового колеса.
| 
| |
| | | | | | | | | | |
| | Тема 8
| МЕХАНИЧЕСКИЕ ВОЛНЫ -процесс распространения колебаний в упругой среде.
|
| | Упругая среда
| ➨вещество, способное подвергаться упругим деформациям.
|
| | Упругие (механические)
волны
| ➨механические возмущения, распространяющиеся в упругой среде.
Примеры: звуковые волны; волны на воде; колебания почвы, распространяющиеся от источника.
Упругие волны бывают поперечными и продольными.
|
| | Поперечные волны

| ➨волны, в которых колебания частиц среды происходят перпендикулярно направлению распространения волны.
Поперечные волны представляют собой чередование горбов и впадин (пример: волны на воде).
|
| | Продольные волны

| ➨волны, в которых колебания частиц среды происходят в направлении распространения волны.
Продольные волны представляют собой чередование областей уплотнений и разрежений (пример: звуковые волны).
|
| | · длина волны
 [м] [м]
| ➨расстояние, на которое волна распространяется за один период, т.е. кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
|
| | · скорость волны
(фазовая скорость)
 [м/с] [м/с]
| ➨скорость распространения колебаний в пространстве;
|
| | · связь между длиной волны, скоростью волны и периодом колебаний
| ➨  , ,  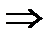

|
| | · уравнение
гармонической волны
 
| ➨ пусть источник волн колеблется по гармоническому закону:  .
Точка, находящаяся на расстоянии х от источника, запаздывает по времени на .
Точка, находящаяся на расстоянии х от источника, запаздывает по времени на  = =  : :  = =  = = 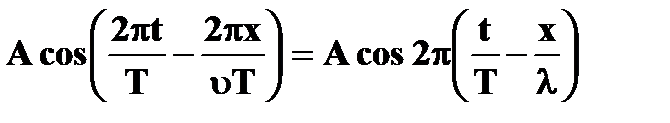
|
| | Тема 9
| ЗВУК
|
| | ЗВУК
| ➨ механическое явление, субъективно воспринимаемое органом чувств человека и животных или
➨ механические колебания и волны в упругих средах (в вакууме механические волны не распространяются);
|
| | · звуковые волны
| ➨ упругие волны, вызывающие у человека ощущение звука; распространяются в газах, жидкостях и твердых телах;
|
| | · классификация
звуковых волн
| инфразвук
до 16 Гц
| звуковой диапазон
16 - 20000 Гц
| ультразвук
более 20000 Гц
|
| | · условия,
необходимые
для возникновения
ощущения звука
| ➨ 1) наличие источника звука; 2) наличие упругой среды между источником и ухом; 3) частота колебаний должна лежать в звуковом диапазоне;
4) мощность звука должна быть достаточной для восприятия.
|
| | · скорость звука
  
| ➨ скорость распространения фазы колебания, т.е. области сгущения или разрежения в волне.
|
| | · зависимость
скорости
распространения звука
| ➨ скорость звука в среде зависит от свойств и состояния среды.. Например:  в воздухе 331,6 м/с (при в воздухе 331,6 м/с (при  ), 340 м/с (при150С);
вдистиллированной воде 1484 м/с; в железе 5170 м/с.
(Е – модуль упругости среды – модуль Юнга; ), 340 м/с (при150С);
вдистиллированной воде 1484 м/с; в железе 5170 м/с.
(Е – модуль упругости среды – модуль Юнга;  - плотность среды) - плотность среды)
|
| | от среды и температуры
|
 
|
| | Характеристики звуковых волн:
|
| | · громкость звука
· высота тона
| ➨ характеризуют слуховые ощущения человека;
➨ громкость звука зависит от амплитуды звуковых колебаний; высота тона – от частоты колебаний.
|
| | · интенсивность (сила)
звука
 
| ➨ количество энергии  , переносимое звуковой волной за время , переносимое звуковой волной за время  =1 с через площадку =1 с через площадку  =1 м2, перпендикулярную направлению распространения волны или отношение звуковой мощности к площади поверхности. =1 м2, перпендикулярную направлению распространения волны или отношение звуковой мощности к площади поверхности.
|
| | · уровень громкости
 [Б] [Б]
 [дБ] [дБ]
| ➨ мера чувствительности органов слуха к восприятию звуковых волн данной интенсивности;
|
| | ➨ определяется как логарифм отношения интенсивности  данного звука к интенсивности звука данного звука к интенсивности звука  порога слышимости. порога слышимости.
|
| | ➨ наименьшее изменение громкости звука, которое может ощущать человек с нормальным слухом, составляет десятую долю бела (Б) – децибел (дБ).
|
| Раздел 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
ЛЕКЦИЯ 7
| |
| МОЛЕКУЛЯРНАЯ ФИЗИКА
‒ раздел физики, изучающий макроскопические свойства тел в
различных агрегатных состояниях на основе рассмотрения их
молекулярного строения
| |
| Тема 10
| МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
ИДЕАЛЬНЫХ ГАЗОВ
| |
| Основные положения
МКТ ▼
| Опытные обоснования
МКТ▼
| |
| ❶ все тела состоят из мельчайших частиц (атомов, молекул);
| ➨ наличие проницаемости, сжимаемости и растворимости свидетельствует о том, что вещества не сплошные, а состоят из отдельных, разделенных промежутками частиц;
| |
| ❷ молекулы находятся в непрерывном тепловом движении;
| ➨ наблюдения броуновского движения и диффузии частиц показали, что молекулы находятся в непрерывном тепловом движении;
| |
| ❸между молекулами существуют силы взаимодействия – (притяжения и отталкивания); природа этих сил электромагнитная.
| ➨ наличие прочности, упругости, смачиваемости, прилипания, поверхностного натяжения в жидкостях доказывает существование сил взаимодействия между молекулами;
| |
| ● тепловое движение
молекул
| ➨ хаотическое движение молекул, атомов и ионов в газах, жидкостях и твердых телах;
| |
| ● броуновское
движение
| ➨ непрерывное хаотическое движение мельчайших твердых частиц, взвешенных в жидкости; служит доказательством существования молекул жидкости и хаотического характера их теплового движения; интенсивность движения зависит от размеров броуновских частиц и температуры среды;
| |
| ● диффузия
| ➨ явление самопроизвольного проникновения молекул одного вещества в межмолекулярное пространство другого вещества при их соприкосновении;
➨ примеры диффузии: в газах – распространение запахов; в жидкостях – перемешивание жидкостей разной плотности (молекулы тяжелой жидкости поднимаются вверх, а более легкой – опускаются вниз); в твердых телах – сращивание двух металлических пластинок в одно целое.
➨ диффузия в жидкостях происходит медленнее, чем в газе, но быстрее, чем в твердых телах и возрастает с повышением температуры;
| |
| Мельчайшие частицы
|
| |
| молекула
| ➨ наименьшая устойчивая частица данного вещества, обладающая его основными химическими свойствами;
| |
| атом
| ➨ наименьшая частица данного химического элемента;
| |
Масса и размер
молекул
 диаметр атома - диаметр атома -  м
а.е.м.= м
а.е.м.=   =1,66·10-27кг
=1,66·10-27кг
| ➨ молекулы вещества состоят из атомов одного или разных химических элементов. Размеры атомов характеризуются диаметром. Наименьший по размерам атом водорода.
Поскольку массы атомов и молекул очень малы, то при расчетах используют не абсолютные, а относительные значения масс, получаемые путем сравнения масс атомов и молекул с атомной единицей массы, в качестве которой выбрана 1/12 часть атома углерода ( =1,995·10-26кг). Причина такого выбора состоит в том, что углерод входит в большое число различных химических соединений. =1,995·10-26кг). Причина такого выбора состоит в том, что углерод входит в большое число различных химических соединений.
| |
Относительная
молекулярная
(атомная) масса

| ➨ равна отношению массы молекулы (или атома)  данного вещества к 1/12 массы атома углерода данного вещества к 1/12 массы атома углерода  (безразмерная величина).
Относительная атомная масса каждого химического элемента указана в таблице Д.И. Менделеева (см. приложение)
Например, относительная атомная масса
водорода 1,00797, кислорода 15,9994; (безразмерная величина).
Относительная атомная масса каждого химического элемента указана в таблице Д.И. Менделеева (см. приложение)
Например, относительная атомная масса
водорода 1,00797, кислорода 15,9994;
| |
| ● относительная
молекулярная
масса вещества
| ➨ относительная молекулярная масса данного вещества  равна сумме относительных атомных масс химических элементов, составляющих молекулы вещества (безразмерная величина);
Пример: равна сумме относительных атомных масс химических элементов, составляющих молекулы вещества (безразмерная величина);
Пример:  молекулы воды Н2О: 2·1+16=18 молекулы воды Н2О: 2·1+16=18
| |
Количество вещества
 [моль]
или [моль]
или
| ➨ число молекул или атомов, содержащихся в теле, равное отношению числа молекул (или атомов) N в данном веществе к числу молекул (атомов) в 1 моле вещества NА;
| |

| ➨ равно отношению массы вещества m к его молярной массе  ; ;
| |
| ● единица измерения
количества вещества
1 моль
| ➨ количество вещества, в котором содержится столько же молекул или атомов, сколько атомов содержится в углероде С массой 0,012 кг;
| |
| ● постоянная
Авогадро
NA = 6,02 · 1023
[моль-1]
| ➨ число атомов, содержащихся в 1 моле любого вещества;

| |
Молярная масса
(1 моля вещества)
 
| ➨ масса одного моля вещества; равна произведению массы одной молекулы  на количество молекул в 1 моле (NА). на количество молекул в 1 моле (NА).
| |
Молярная масса
(молекулы вещества)
 [кг/моль] [кг/моль]
| ➨ Пример: масса молекулы водорода
 (Н2О) = (Н2О) =  = 18·10 -3 кг/моль = 18·10 -3 кг/моль
| |
Масса вещества
 [кг] [кг]
| ➨ равна произведению массы одной молекулы  на число молекулN в теле. на число молекулN в теле.
| |
Концентрация
молекул в веществе
 
| ➨ численно равна отношению количества молекул N к объему вещества V;
| |
| Скорость
молекул газа
| ➨ скорость движения молекул опытным путем была определена в 1920 г. немецким физиком Отто Штерном;
| |
● опыт Штерна
 1 –внешний
цилиндр;
2 – внутренний
цилиндр;
3 –серебряная
проволока;
4 – узкая щель.
1 –внешний
цилиндр;
2 – внутренний
цилиндр;
3 –серебряная
проволока;
4 – узкая щель.

| ➨ цилиндры неподвижны: серебряную проволоку нагревают до высокой температуры, пропуская по ней электрический ток; атомы серебра, испаряясь с проволоки, заполняют внутренний цилиндр, попадают через щель на внутреннюю поверхность внешнего цилиндра и откладываются в точке В в виде узкой полоски; цилиндры вращаются:  =const; атомы пролетают расстояние АВ = =const; атомы пролетают расстояние АВ =  = (R-r) за время tи осаждаются в виде полоски в точке С. Расстояние между местами осаждения атомов- S. = (R-r) за время tи осаждаются в виде полоски в точке С. Расстояние между местами осаждения атомов- S.
 = =  - средняя скорость движения атомов; - средняя скорость движения атомов;
 ; ;  = =  (линейная скорость наружного цилиндра); (линейная скорость наружного цилиндра);
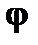  - (угол поворота цилиндров) - (угол поворота цилиндров) 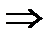 
 = =  = 650 м/с = 650 м/с
| |
 Взаимодействие молекул Взаимодействие молекул
| ➨ во всех телах (твердых, жидких, газообразных) молекулы взаимодействуют друг с другом.
Доказательством наличия сил являются:
взаимное притяжение - способность твердого тела сопротивляться растяжению; взаимное отталкивание - поверхностное натяжение жидкостей; способность жидких, твердых тел и уплотненных газов сопротивляться сжатию. Одновременное действие сил притяжения и отталкивания не позволяют частицам, образующим тела, разлетаться в разные стороны или «слипаться»;
| |
рис.1

| ➨ межмолекулярное взаимодействие имеет электрическую природу, хотя молекула в целом электрически нейтральна, т.к. суммы «+» и «-» зарядов в ней равны; электрическое поле за пределами молекулы быстро убывает. На расстоянии r > 2-3 диаметров поле молекулы можно считать равным нулю; силы взаимодействия между молекулами малы (рис.1);
| |
рис. 2
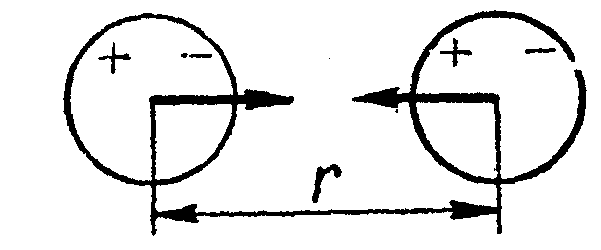
| ➨ при сближении молекул возникает взаимодействие электрических зарядов ядер и электронных оболочек молекул; разноименные заряды притягиваются, одноименные – отталкиваются; между молекулами возникают силы притяжения (рис.2);
| |
 рис. 3 рис. 3
| ➨ когда молекулы «соприкоснутся» своими электронными оболочками, дальнейшее сближение станет невозможным и возникнут большие силы отталкивания (рис.3);
| |
| Модели
| ➨ молекулы газа находятся на расстояниях r>> dдиаметрасамих молекул; частицы газа не связаны молекулярными силами притяжения; газы могут легко сжиматься и неограниченно расширяться; не имеют постоянного объема;
| |
| ● газа
| |
| ● жидкости
| ➨ расстояния между молекулами меньше, чем в газах; силы взаимодействия между молекулами велики; при сжатии жидкостей возрастают силы отталкивания; жидкости малосжимаемы; имеют определенный объем;
| |
| ● твердого тела
| ➨ расстояния между молекулами меньше, чем в жидкостях; если при сжатии твердого тела молекулы сближаются на расстояниеr < dмолекулы, то возникают большие силы отталкивания, которые препятствуют растяжению и способствуют возвращению частиц в первоначальное положение; твердые тела имеют постоянную форму и объем;
| |
| Идеальный газ
(теоретическая модель)
| ➨ газ, размерами молекул которого можно пренебречь и считать, что потенциальная энергия взаимодействия молекул на расстоянии равна нулю;
| |
Основное уравнение
МКТ

| ➨ определяет связь между давлением р газа, массой его отдельных молекул  , концентрацией молекул , концентрацией молекул  и средней квадратичной скоростью движения молекул и средней квадратичной скоростью движения молекул 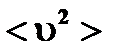 ; ;
| |

| ➨ связь давления со средней кинетической энергией молекул; 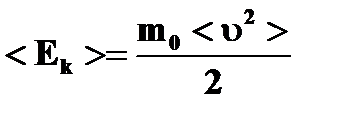 - средняя кинетическая энергия поступательного движения молекул; - средняя кинетическая энергия поступательного движения молекул;
| |

| ➨ зависимость давления газа от концентрации молекул;
| |
Закон Дальтона

| ➨ давление в газовой смеси равно сумме парциальных давлений всех газов, входящих в эту смесь;
| |
| ● парциальное
давление
| ➨ давление, которое имел бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси, при той же температуре;
| |
● средняя
квадратичная
скорость
 
| ➨  = =  ; ;
| |
| ● кинетическая
энергия частиц газа
|
➨ 
| |
● постоянная
Больцмана
 = 1,38·10-23
[Дж/К] = 1,38·10-23
[Дж/К]
| ➨ показывает, насколько изменится кинетическая энергия одной молекулы при изменении температуры на один градус;
➨ равна отношению универсальной газовой постоянной R к постоянной АвогадроNA;
| |
Уравнение
Клапейрона
 или
или

| ➨ при переходе из одного состояния в другое данной массы газа произведение давления на объем, деленное на абсолютную температуру, есть величина постоянная;
| |
Уравнение
Клапейрона-
Менделеева

| ➨ уравнение состояния идеального газа;
➨ для 1 моля газа;
| |
Уравнение
Клапейрона-
Менделеева

| ➨ уравнение показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа.
➨ для произвольной массы газа;
| |
| ● универсальная
газовая постоянная
R= 8,31 Дж/моль·К
| ➨ численно равна работе, совершенной одним молем идеального газа при изобарном повышении температуры на один градус(1 К)

| |
| ИЗОПРОЦЕСС
| ➨ процесс, протекающий в системе с неизменной массой при постоянном значении одного из параметров состояния системы
– температуре Т,
– давлении р,
– объеме V;
| |
ИЗОТЕРМИЧЕСКИЙ
процесс
● закон
Бойля - Мариотта
 T = const
m = const
T = const
m = const
|  ➨ для данной массы газапри постоянной температуре T произведение численных значений давления p и объема Vесть величина постоянная; ➨ для данной массы газапри постоянной температуре T произведение численных значений давления p и объема Vесть величина постоянная;
| |
ИЗОБАРНЫЙ
процесс
● закон
Гей Люссака
 р = const
m = const
р = const
m = const
| ➨ для данной массы газапри постоянном давлении p, объем V идеального газа прямо пропорционален его абсолютной температуре T.

| |
ИЗОХОРНЫЙ
процесс
● закон Шарля
 V = const
m = const
V = const
m = const
|  ➨ для данной массы газапри постоянном объеме V, давление pгаза прямо пропорционально Т ➨ для данной массы газапри постоянном объеме V, давление pгаза прямо пропорционально Т
| |
Адиабатный процесс

| ➨ процесс, при котором отсутствует теплообмен между системой и окружающей средой
 ;
➨ ;
➨  - показатель адиабаты; - показатель адиабаты;
| 
| |
| | | | | | | | | | | |