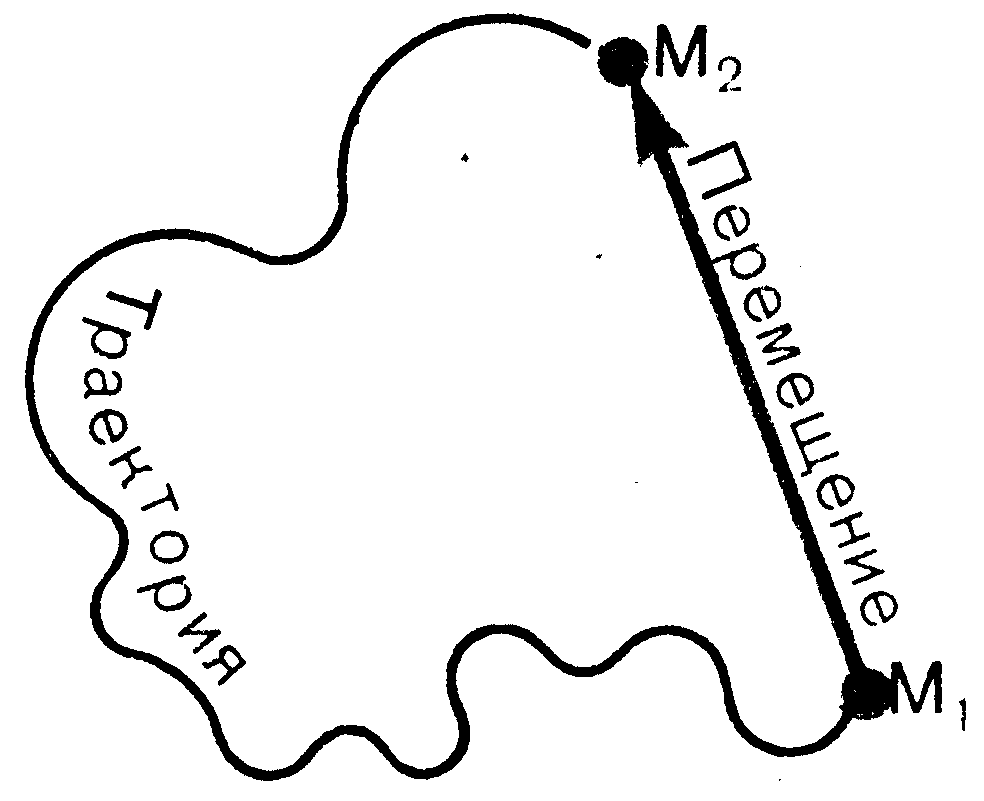
| | ТРАЕКТОРИЯ
| †линия, которую описывает материальная точка (или тело) при своем движении;
По траектории различают два вида движения: поступательное и вращательное.
|
| | ПУТЬ ∆S [м]
| † положительная скалярная величина, не убывающая со временем;
† расстояние ∆S, пройденное материальной точкой (телом) по её траектории;
† пути, пройденные точкой (телом) за последовательные промежутки времени, складываются арифметически;
† ∆S= 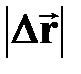 пройденный путь равен модулю перемещения при прямолинейном движении в одном направлении;
По характеру зависимости пути от времени движения делятся на равномерные и неравномерные. пройденный путь равен модулю перемещения при прямолинейном движении в одном направлении;
По характеру зависимости пути от времени движения делятся на равномерные и неравномерные.
|
| | 
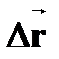 ∆S
∆S
|
| | ПЕРЕМЕЩЕНИЕ 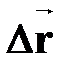 [м] [м]
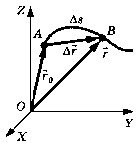
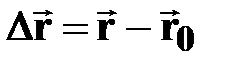
| † направленный отрезок, проведенный из начальной точки М1 в заданную точку М2 траектории (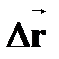 - вектор)
† векторы перемещений складываются
геометрически: если материальная точка (тело) одновременно участвует в нескольких движениях, то результирующее перемещение равно векторной сумме перемещений, совершаемых точкой (телом) в каждом из движений; - вектор)
† векторы перемещений складываются
геометрически: если материальная точка (тело) одновременно участвует в нескольких движениях, то результирующее перемещение равно векторной сумме перемещений, совершаемых точкой (телом) в каждом из движений;
|
| |
|
|
| | ПОСТУПАТЕЛЬНОЕ движение
† движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе;
† траектории всех точек тела одинаковые;
|
| | |
|
| | СКОРОСТЬ
| † быстрота изменения перемещения со временем;
† определяет направление тела в данный момент времени;
† векторная физическая величина;
|
| | Средняя скорость
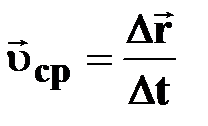 [м/с] [м/с]
| † отношение перемещения 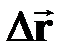 к промежутку времени к промежутку времени  , в течение которого это перемещение произошло;
† вектор средней скорости , в течение которого это перемещение произошло;
† вектор средней скорости 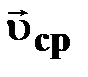 совпадает с направлением вектора перемещения совпадает с направлением вектора перемещения 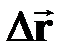 ; ;
|
| | — модуль
средней скорости
(средняя путевая скорость)
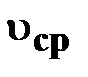 = = 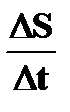 [м/с] [м/с]
| † отношение пройденного пути ΔS за промежуток времени Δt
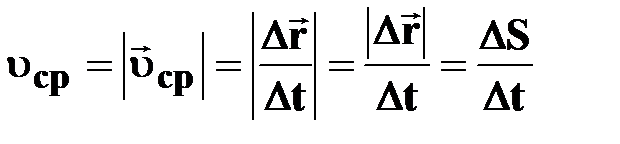 † скалярная величина;
† скалярная величина;
|
| | Мгновенная скорость
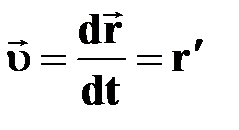 [м/с] [м/с]
| † скорость в данный момент времени (в данной точке траектории);
† предел (Ɩim), к которому стремится средняя скорость  за бесконечно малый промежуток времени Δt за бесконечно малый промежуток времени Δt
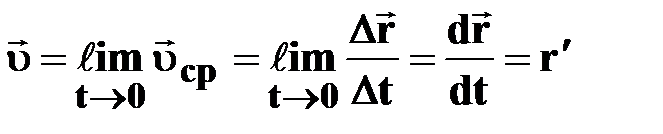 †
† 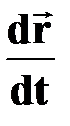 = = 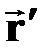 - первая производная перемещения по времени;
† вектор мгновенной скорости - первая производная перемещения по времени;
† вектор мгновенной скорости 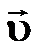 направлен по касательной к траектории в сторону движения; направлен по касательной к траектории в сторону движения;
|
| | — модуль
мгновенной скорости
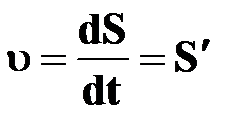 [м/с] [м/с]
| † 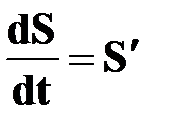 - первая производная пути по времени; - первая производная пути по времени;
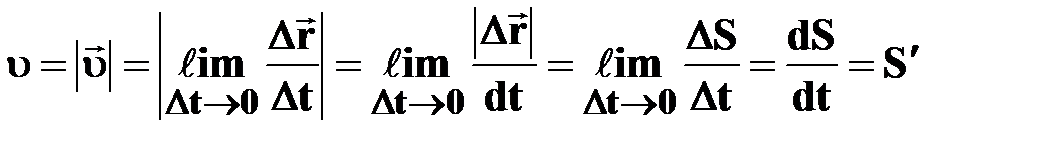 † скалярная величина;
† скалярная величина;
|
| | УСКОРЕНИЕ
| † характеристика неравномерного движения;
† быстрота изменения скорости со временем;
† векторная физическая величина;
|
| | Среднее ускорение
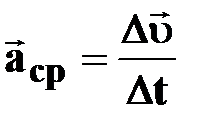 [м/с2] [м/с2]
| †  -изменение скорости за промежуток
времени -изменение скорости за промежуток
времени 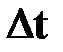 ;
† векторная физическая величина; ;
† векторная физическая величина;
|
| | Мгновенное ускорение
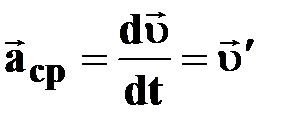 [м/с2] [м/с2]
| † ускорение в данный момент времени;
†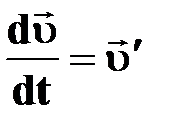 первая производная скорости по времени;
† предел (Ɩim), к которому стремится среднее ускорение первая производная скорости по времени;
† предел (Ɩim), к которому стремится среднее ускорение 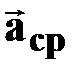 за бесконечно малый промежуток времени Δt за бесконечно малый промежуток времени Δt
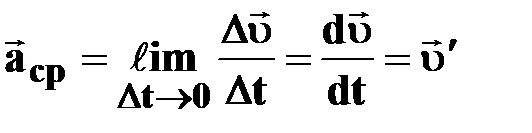
|
| | СОСТАВЛЯЮЩИЕ УСКОРЕНИЯ
|
| | —тангенциальное
ускорение
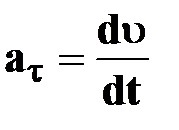 [м/с2] [м/с2]
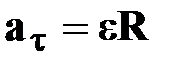
| † характеризует быстроту изменения скорости по модулю;
†  направлено по касательной к траектории;
†т.к. направлено по касательной к траектории;
†т.к. 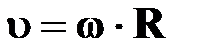 , , 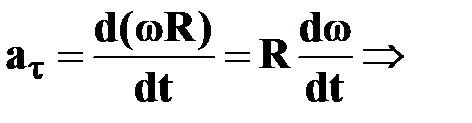 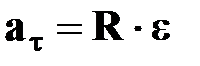
| 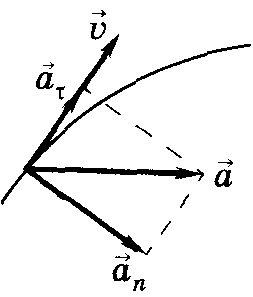
|
| | — нормальное
ускорение
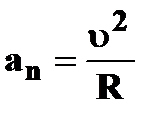 или или 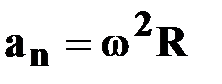 [м/с2] [м/с2]
| † характеризуетбыстроту изменения скорости по направлению;
† 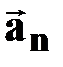 направлено к центру кривизны траектории радиусом R.
†т.к. направлено к центру кривизны траектории радиусом R.
†т.к. 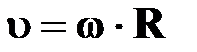 , , 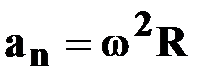
|
| | Полное ускорение
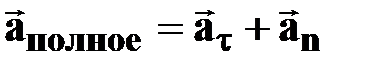
| † геометрическая сумма тангенциальной 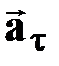 и нормальной
и нормальной 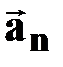 составляющих; составляющих;
|
| | — модуль
полного ускорения
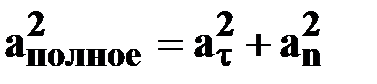 [м/с2] [м/с2]
|
† 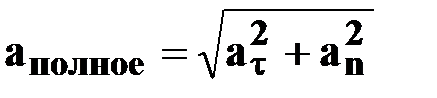 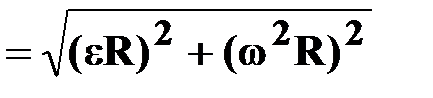 ; ;
|
| | ПРИМЕРЫ РАЗЛИЧНЫХ ВИДОВ ДВИЖЕНИЯ
|
| | РАВНОМЕРНОЕ
движение
| † движение, при котором материальная точка (тело) за любые равные промежутки времени совершает одинаковые перемещения;
|
| | ПРЯМОЛИНЕЙНОЕ движение
| † движение, при котором траектория
материальной точки – прямая линия;
|
| | РАВНОМЕРНОЕ
ПРЯМОЛИНЕЙНОЕ
движение
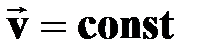 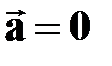
| † движение с постоянной по модулю и направлению скоростью;
† средняя скорость  равна мгновенной скорости равна мгновенной скорости 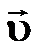 ; ;
|
| | ПУТЬ
| † 
| х0, х –начальная и конечная
координаты;
|
| | ПЕРЕМЕЩЕНИЕ
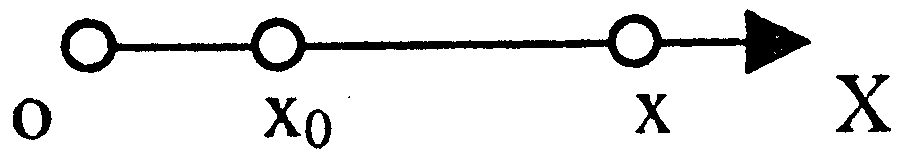
| † 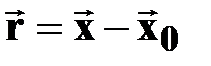
|
| | † 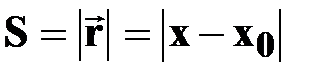 - путь равен модулю вектора перемещения при движении точки по прямой линии в одном направлении; - путь равен модулю вектора перемещения при движении точки по прямой линии в одном направлении;
|
| | Скорость средняя
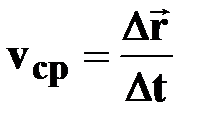 [м/с] [м/с]
| † 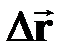 - перемещение точки за промежуток времени - перемещение точки за промежуток времени  ;
† направление ;
† направление 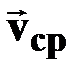 совпадает с направлением совпадает с направлением 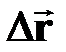 ;
† векторная величина; ;
† векторная величина;
|
| | Модуль
средней скорости
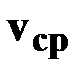 = = 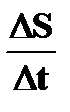 [м/с] [м/с]
| ➨ отношение пройденного пути S к промежутку времени t, за который этот путь пройден;
† скалярная величина;
|
| | Уравнение
координаты
| 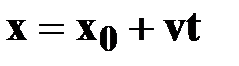
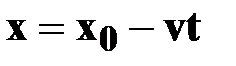
| ➨ - вектор скорости  и ось ОХсонаправлены;
➨ - вектор скорости и ось ОХсонаправлены;
➨ - вектор скорости  и ось ОХпротивоположны; и ось ОХпротивоположны;
|
| | Графическое
представление
равномерного
прямолинейного
движения
| 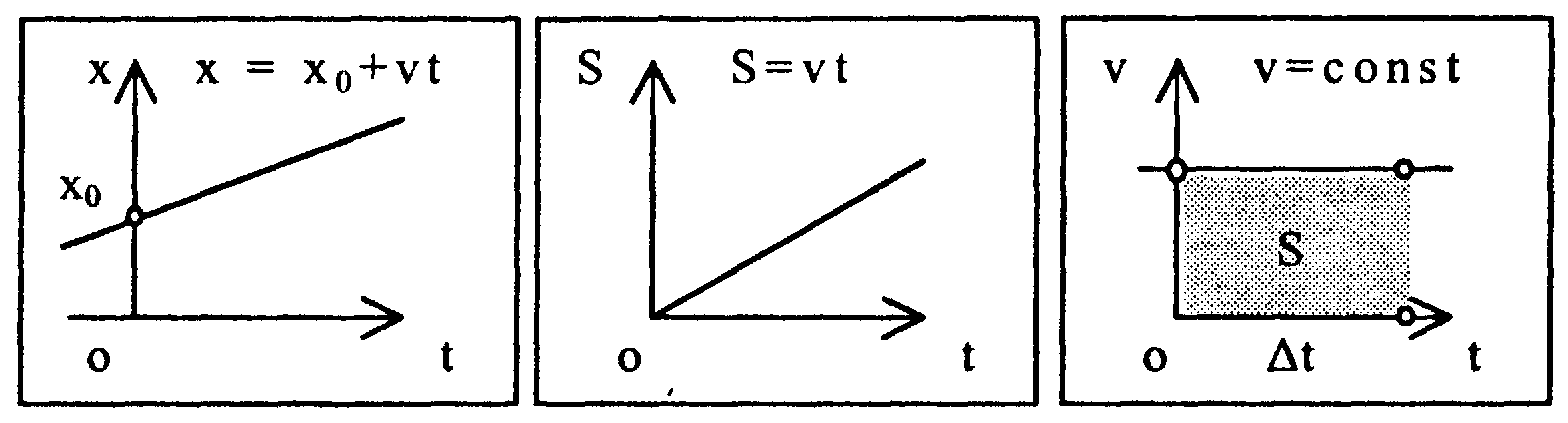
|
РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ
движение
 
| † прямолинейное движение материальной точки, при котором ее ускорение 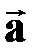 с течением времени остается постоянным; с течением времени остается постоянным;
|
РАВНОУСКОРЕННОЕ прямолинейноедвижение† движение, при котором за любые равные промежутки времени скорость материальной точки увеличивается на одну и ту же величину
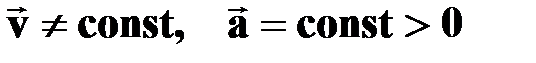
| РАВНОЗАМЕДЛЕННОЕ прямолинейноедвижение† движение, при котором за любые равные промежутки времени, скорость материальной точки уменьшается на одну и ту же величину
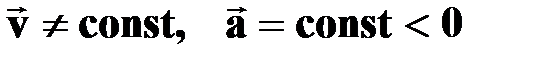
|
Среднее ускорение
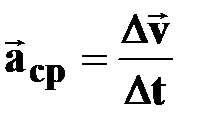 [м/с2] [м/с2]
| † 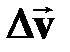 -изменение скорости за промежуток
времени -изменение скорости за промежуток
времени 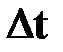 ;
† векторная физическая величина; ;
† векторная физическая величина;
|
Мгновенное ускорение
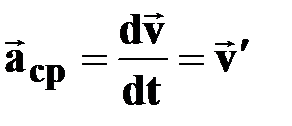 [м/с2] [м/с2]
|
†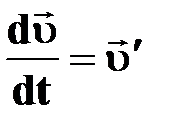 первая производная скорости по времени; первая производная скорости по времени;
|
Уравнение скорости
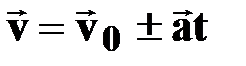 [м/с] [м/с]
| † векторная форма записи;
|
Уравнение координаты
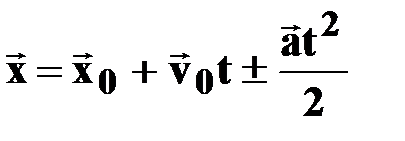
| † векторная форма записи;
† в проекциях на ось ОХ: х0>0, v0>0, a>0,
т.к. векторы 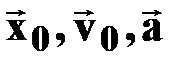 сонаправлены с осью ОХ;
† в проекциях на ось ОХ: х0>0, v0>0, a<0,
т.к. векторы сонаправлены с осью ОХ;
† в проекциях на ось ОХ: х0>0, v0>0, a<0,
т.к. векторы 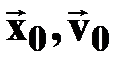 сонаправлены с осью ОХ; вектор сонаправлены с осью ОХ; вектор 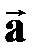 направлен противоположно оси ОХ; направлен противоположно оси ОХ;
|
| Уравнение пути
| 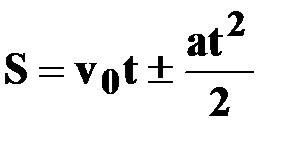 [м] [м]
|
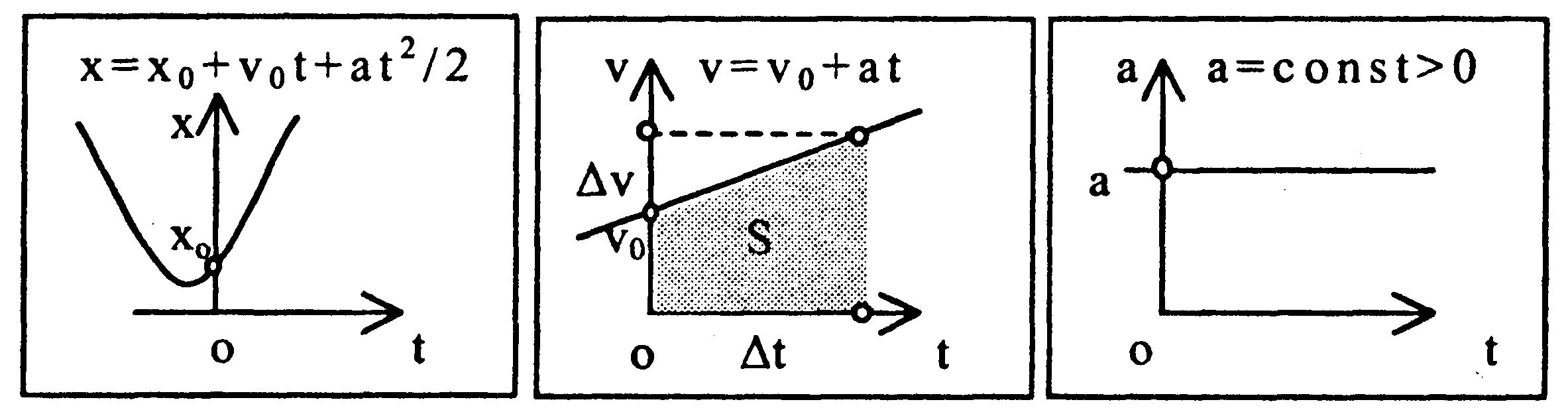
| Графическое
представление
равноускоренного
прямолинейного
движения
| 
|
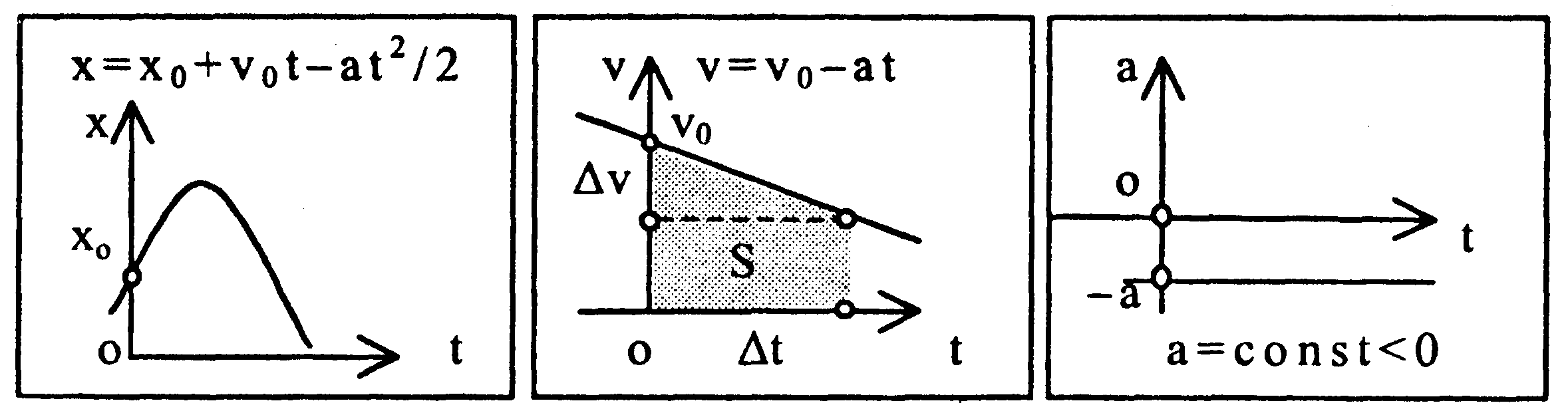
| Графическое
представление
равнозамедленного
прямолинейного
движения
| 
|
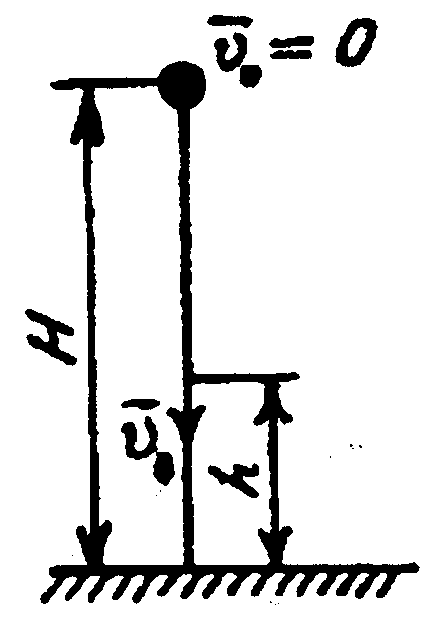
| СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
† движение тела под действием силы тяжести;
† свободное падение является равнопеременным движением (пренебрегая со
противлением воздуха);
|
| ● ускорение
свободного
падения
g = 9,81 м/с2
| † всегда направлено к центру Земли;
† gсонаправлено с ОУ;
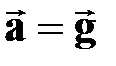 <0 - равнозамедленное –
при движении вверх; <0 - равнозамедленное –
при движении вверх;
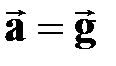 >0 - равноускоренное –
при движении вниз; >0 - равноускоренное –
при движении вниз;
|
| ● уравнение координаты
| 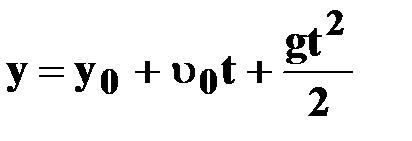
| 
| 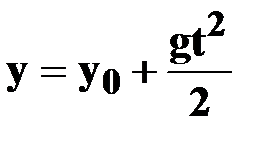
|
| ● уравнение пути
(S=h)
| 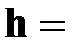 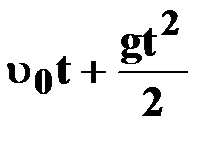
| 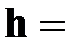 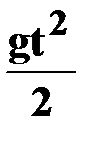
|
| ● уравнение скорости
| 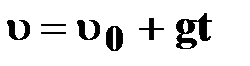
| 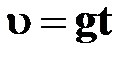
|
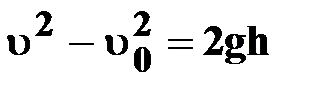
| 
|
| ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
|
| ● уравнение координаты
а=-g= - 9,81 м/с2
| 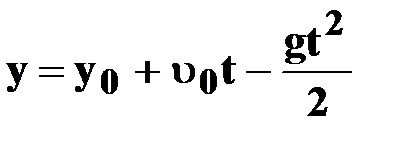
|
| ● уравнение пути
(S=h)
| 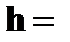 
|
| ● уравнение скорости
| 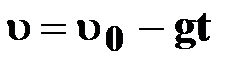 ; ;
| При 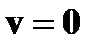  за время
за время
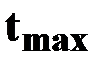 ,
тело достигнет максимальной высоты ,
тело достигнет максимальной высоты
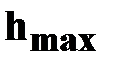
| 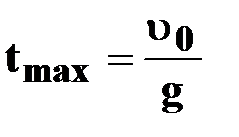
|
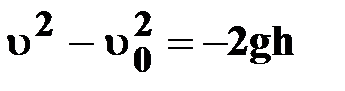
| 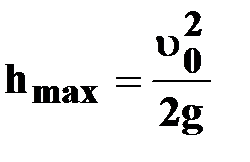
|
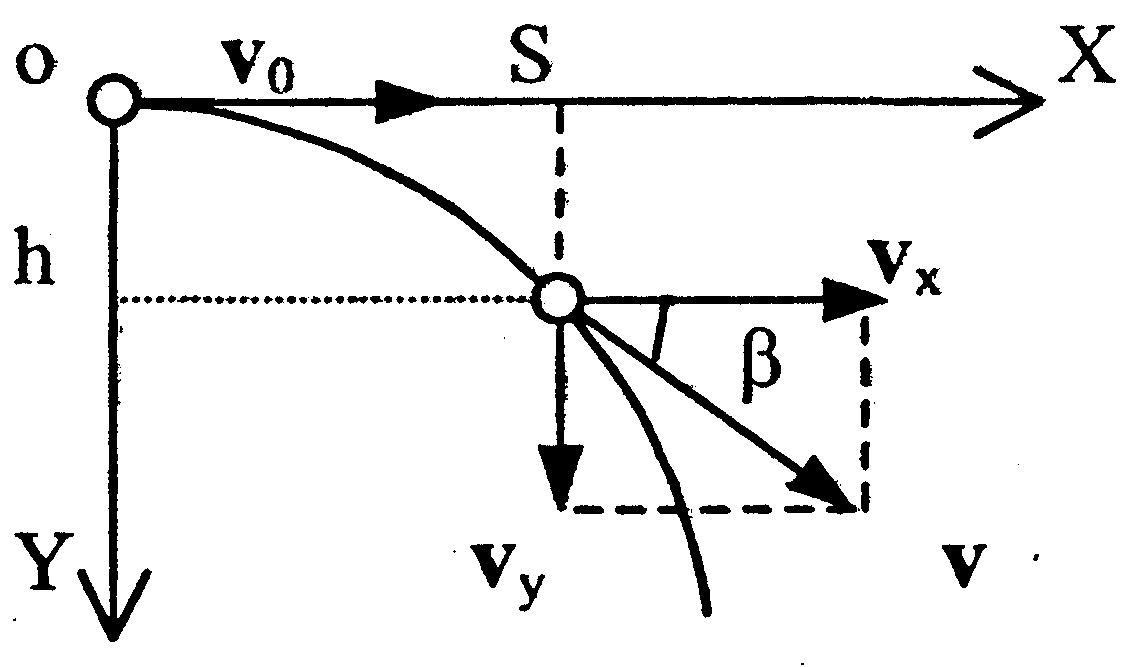
| ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО
|
| Закон
независимости
движений
| † если материальная точка участвует одновременно в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом движении.
|
➨ вдоль оси ОХ – равномерное движение (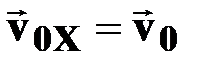 )
➨ вдоль ОУ – свободное падение ( )
➨ вдоль ОУ – свободное падение (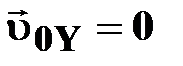 ) )
|
| ● мгновенная скорость
| 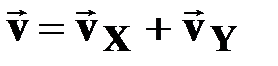
| 
|
| ● горизонтальная
скорость
| 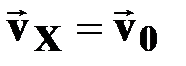
|
| ● вертикальная
скорость
| 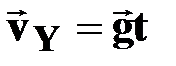
|
| ● модуль
скорости
| 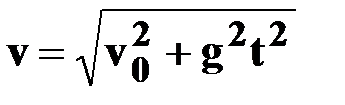
|
| ● уравнение координат
точки
| 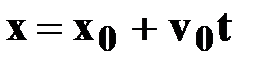
| 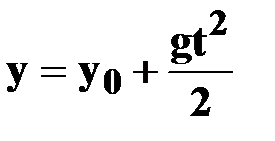
| 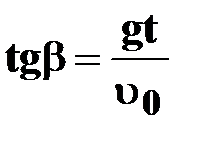 g = 9,81 м/с2
g = 9,81 м/с2
|
| ● уравнение пути (S=h)
| 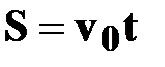
| 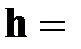 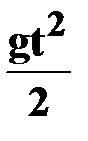
|
| ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ
|
➨ вдоль оси ОХ – равномерное движение 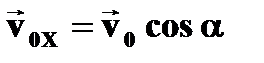 ➨ вдоль ОУ – равнопеременное движение
➨ вдоль ОУ – равнопеременное движение 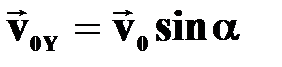
|
до высоты 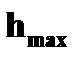 :
движение
равнозамедленное,
затем –
равноускоренное. :
движение
равнозамедленное,
затем –
равноускоренное.
| 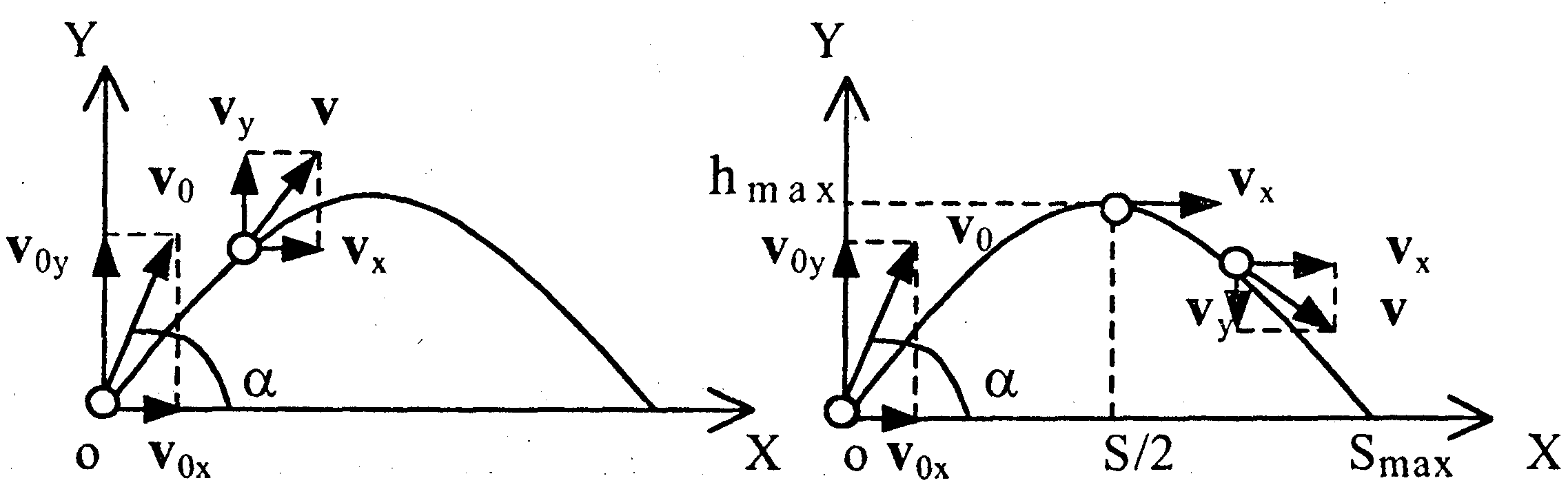
|
| ● уравнения
координат точки
| 
| 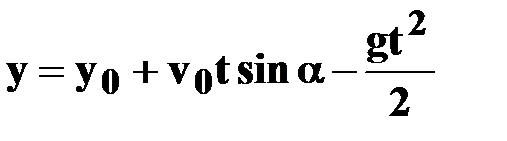
|
| ● уравнения
перемещений
| 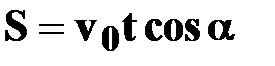
| 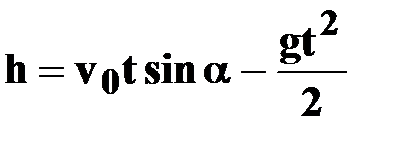
|
| ● уравнения скорости
| 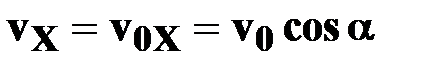
| 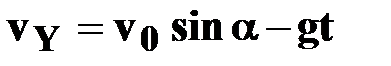
|
| ● модуль скорости
| 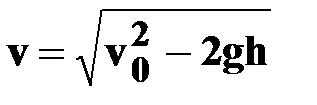
|
● время подъема на
максимальную высоту
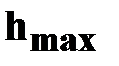
| 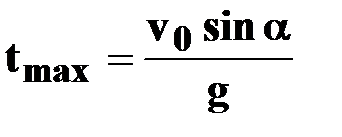
|
| ● максимальная
высота подъема
| 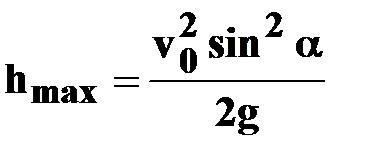
|
| ● максимальный
путь
| 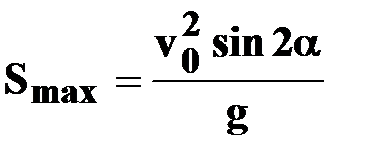
|
| РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
|
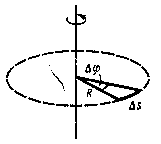
| Движение
по окружности
| † точка Мдвижется по окружности радиуса R. За время tточка прошла дугуМ1М2. Радиус поворачивается на угол 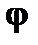 ; ;
| 
|
●; частота вращения
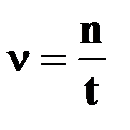 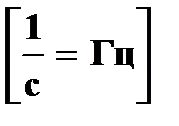
| † физическая величина, равная отношению количества  оборотов ко времени оборотов ко времени 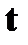 , за которое они совершены; , за которое они совершены;
|
| ●; единица частоты
Герц [Гц]
| † частота, при которой тело совершает один оборот за одну секунду;
|
●; период вращения
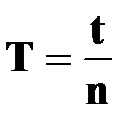 [с] [с]
| † время, за которое точка совершает один полный оборот вокруг оси вращения (на угол 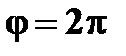 радиан) радиан)
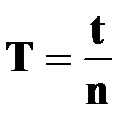  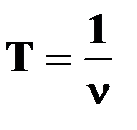 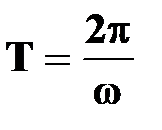
|
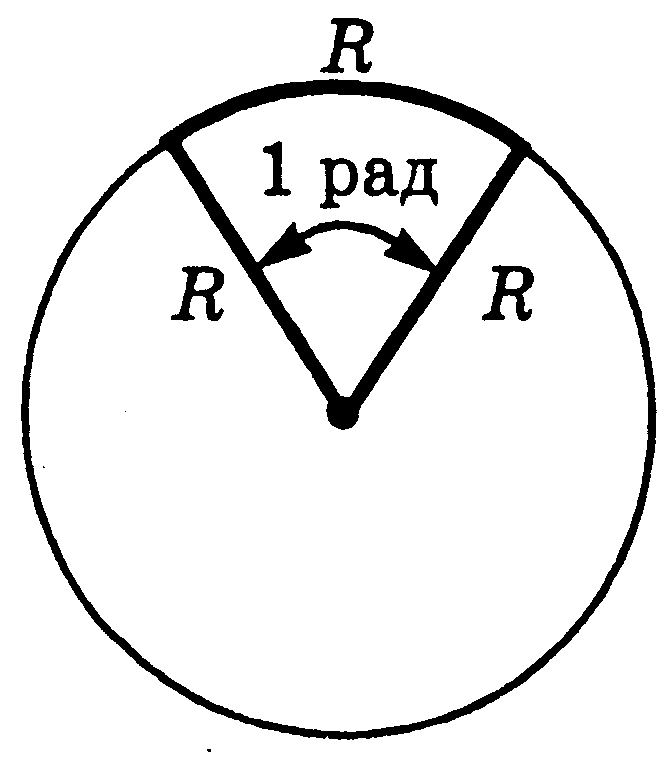
●; радиан (рад)
(единица плоского угла)
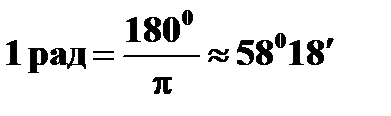
| † равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу. В градусном исчислении:
| 
|
● угловая скорость
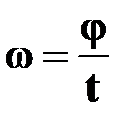 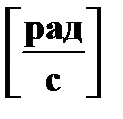
| † физическая величина, равная отношению угла поворота 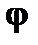 ко времени ко времени 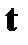 , за которое поворот произошел;
† при одном обороте точка М опишет угол , за которое поворот произошел;
† при одном обороте точка М опишет угол
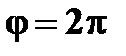 радиан радиан 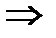
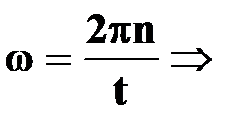 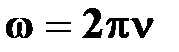 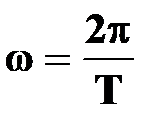
|
— линейная скорость
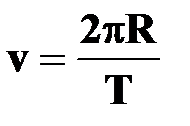 или или 
| † линейная скорость точки, равномерно движущейся по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории;
† 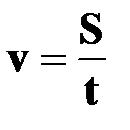 ( (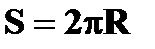 - длина окружности) - длина окружности) 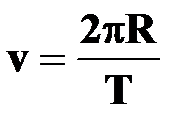
|
| — связь между линейной
и угловой скоростью
| † 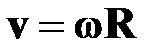
|
Центростремительное
ускорение
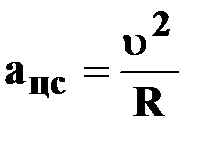 или
или
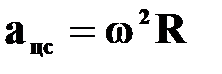
| † при равномерном движении тела по окружности его ускорение постоянно по модулю и в любой точке направлено по радиусу к центру окружности;
|
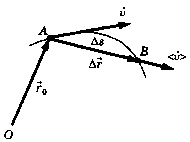
●; вывод формулы
центростремительного
ускорения
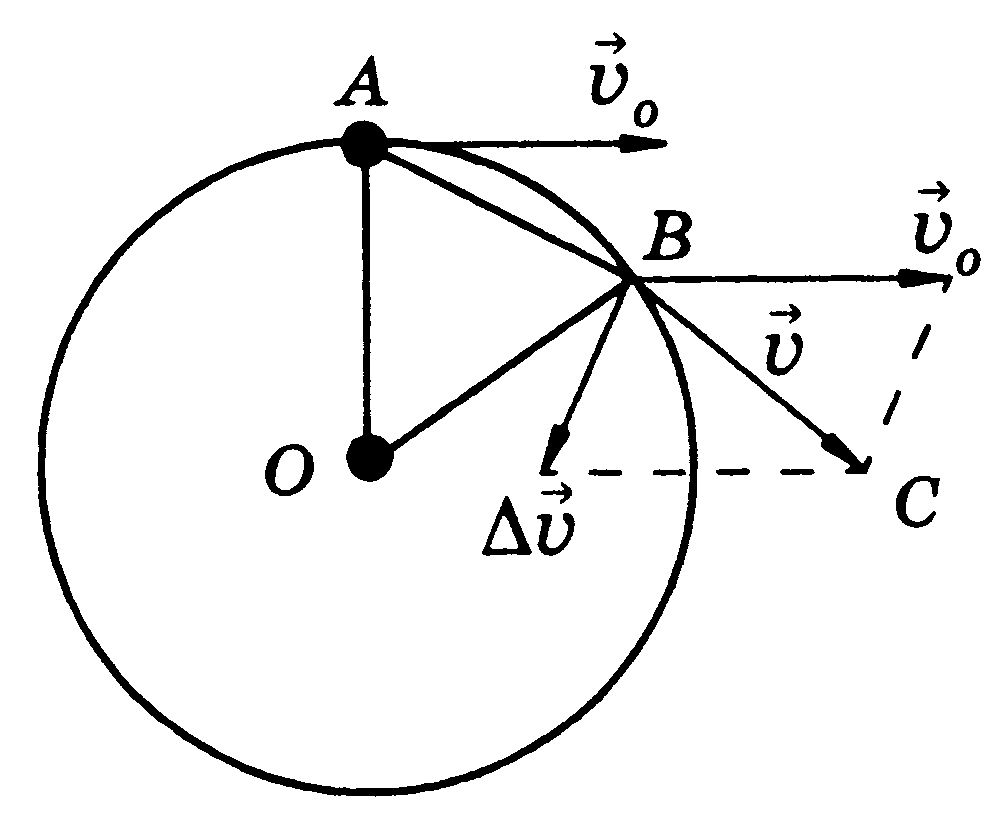
| † в момент времени 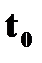 тело находилось в точке А и имело скорость тело находилось в точке А и имело скорость 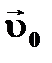 . Через промежуток времени . Через промежуток времени 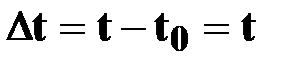 оно переместилось в точку В и имело скорость оно переместилось в точку В и имело скорость 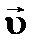 .
Изменение скорости найдем по правилу вычитания векторов: в точку В перенесем вектор .
Изменение скорости найдем по правилу вычитания векторов: в точку В перенесем вектор 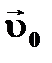 и вычтем его из вектора и вычтем его из вектора 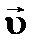 (что равноценно сложению векторов (что равноценно сложению векторов 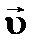 и и 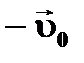 ).
Треугольники АОВ и ВСD подобны и имеют равные углы ).
Треугольники АОВ и ВСD подобны и имеют равные углы 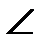 АОВ= АОВ= 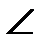 СВD (углы со взаимно перпендикулярными сторонами) СВD (углы со взаимно перпендикулярными сторонами)  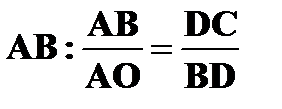 .
Хорда АВ мала, поэтому ее можно заменить дугой АВ, длина которой равна: АВ= .
Хорда АВ мала, поэтому ее можно заменить дугой АВ, длина которой равна: АВ= 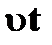 (т.е. произведение скорости на время движения тела от точки А до точки В).
Т.к. АО=R, DC= (т.е. произведение скорости на время движения тела от точки А до точки В).
Т.к. АО=R, DC= 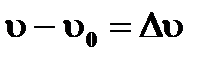 BD=
BD=    ; ; 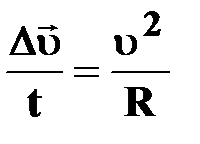 ; ;  
 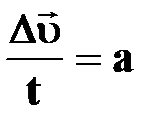  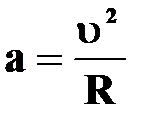
|
|
|
| ЛЕКЦИЯ 2
ВРАЩАТЕЛЬНОЕ движение
движение, при котором траектории всех точек вращающегося тела являются окружностями, центры которых лежат на одной оси, называемой осью вращения
|
| |
| АНАЛОГИЯ
между ПОСТУПАТЕЛЬНЫМ и ВРАЩАТЕЛЬНЫМ движениями
Кинематические характеристики движения
|
| ПОСТУПАТЕЛЬНОЕ
движение
| ВРАЩАТЕЛЬНОЕ
движение
|
| Путь
| S
| м
| Угол
поворота
| j
| рад
|
| Время
| t
| с
| Время
| T
| с
|
| Cкорость
| υ
| м/с
| Угловая
скорость
| w
| рад/с
|
| Ускорение
| а
| м/с2
| Угловое
Ускорение
| e
| рад/с2
|
| Основные кинематические характеристики
ВРАЩАТЕЛЬНОГО движения
|
| УГЛОВАЯ СКОРОСТЬ
| † характеризует быстроту ращения тела;
† векторная величина;
|
Средняя
угловая скорость
 [рад/с] [рад/с]
| †отношение угла поворота  радиус-вектора точки за промежуток времени радиус-вектора точки за промежуток времени  к длительности этого промежутка:
† векторная величина, к длительности этого промежутка:
† векторная величина,
| 
|
Мгновенная
угловая скорость
 [рад/с] [рад/с]
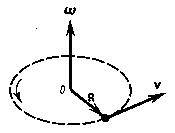
| † вектор, определяемый первой производной угла поворота тела по времени

| 
|
| Направление
угловой скорости
(правило
правого винта)
| † вектор угловой скорости 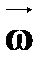 совпадает по направлению с поступательным движением острия винта, который вращается в направлении движения точки по окружности. совпадает по направлению с поступательным движением острия винта, который вращается в направлении движения точки по окружности.
|
| — радиан в секунду
(рад/с)
| † равен угловой скорости равномерно вращающегося тела, все точки которого за 1 с поворачиваются на угол 1 рад.
|
Период вращения
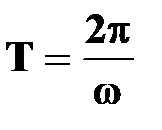 [с] [с]
| † время, за которое точка совершает один полный оборот вокруг оси вращения, т.е. поворачивается на угол 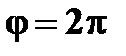 радиан;
† так как промежутку времени радиан;
† так как промежутку времени 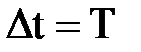 соответствует соответствует 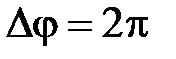 , то , то
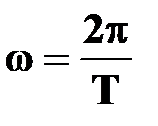
|
Частота вращения
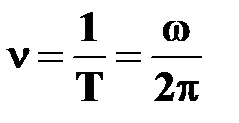 [c-1] [c-1]
| †число полных оборотов, совершаемых телом при его равномерном движении;
† 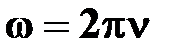
|
УГЛОВОЕ УСКОРЕНИЕ
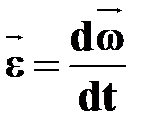 [рад/с2] [рад/с2]
| †векторная величина, равная первой производной угловой скорости по времени:
|
| — радиан на секунду
в квадрате (рад/с2)
| † равен угловому ускорению равноускоренно вращающегося тела, при котором оно за 1с изменяет угловую скорость на 1 рад/с;
|
| Направление
углового ускорения
| †вектор углового ускорения  направлен по оси вращения в сторону вектора элементарного приращения угловой скорости; направлен по оси вращения в сторону вектора элементарного приращения угловой скорости;
|
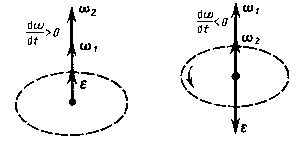
|
при ускоренном движении вектор 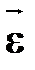 параллелен вектору
параллелен вектору 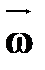
| при з амедленном –
антипараллелен
|
| Связь между
линейными и угловыми характеристиками
| † связь между длиной пути S, пройденного точкой по окружности радиуса R и углом поворота φ
S=φ·R [м]
†связь между линейной скоростью vи угловой скоростью ω
v=ω·R[м/с]
|
Равномерное
вращение
ω=const; 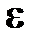 =0 =0
| Равно ускоренное и равно замедленное
вращение
ω≠const; 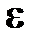 >0 и ω≠const; >0 и ω≠const; 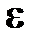 <0 <0
|
Уравнение координаты
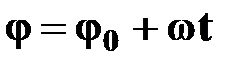
| Уравнение координаты
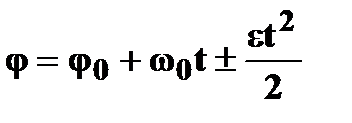
| Уравнение скорости
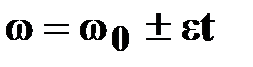
|
φ– угол поворота;
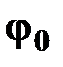 - начальное угловое перемещение;
t – время; - начальное угловое перемещение;
t – время;
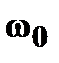 - начальная угловая скорость;
ε-угловое ускорение; - начальная угловая скорость;
ε-угловое ускорение;
|
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | |