Концепція та методичний інструментарій оцінки грошей у часі та концепція та методичний інструментарій урахування фактору інфляції
Визначивши сутність концепції вартості грошей у часі, а також основні чинники, які впливають на вартість грошей, слід безпосередньо перейти до методичного інструментарію, який дає змогу зорієнтуватися у реальній вартості грошей у різні часові періоди. Базовими поняттями, які застосовуються в рамках концепції вартості грошей у часі, є майбутня (нарощена) і теперішня (приведена) вартість грошей. Майбутня вартість грошей – сума інвестованих в даний момент грошових коштів, в яку вони перетворяться через певний період часу з урахуванням певної ставки відсотку. Визначення майбутньої вартості грошей пов’язано з процесом нарощення вартості грошових активів, який являє собою поетапне їх збільшення шляхом приєднання до початкового їх розміру суми відсотку (відсоткових платежів). Теперішня вартість грошей – сума майбутніх грошових коштів, приведених з урахуванням певної ставки відсотку (дисконтної ставки) до теперішнього періоду. Визначення теперішньої вартості грошей пов’язано з процесом дисконтування їх вартості у часі, яке являє собою операцію, обернену нарощенню при обумовленому майбутньому розмірі грошових коштів. Така ситуація виникає в тих випадках, коли необхідно визначити, скільки грошових коштів слід інвестувати сьогодні, для того щоб через певний період отримати наперед обумовлену їх суму. Процеси нарощення і дисконтування можуть здійснюватися як за простими, так і за складними відсотками. Прості відсотки – це відсотки, що нараховуються на початкову суму інвестованих коштів протягом всього періоду нарахування. Складні відсотки – відсотки, що нараховуються не тільки на початкову суму внеску, але також і на всю суму відсотків, накопичених за певний період. В цьому випадку відбувається капіталізація відсотків протягом періоду їх нарахування. Нарахування простих відсотків застосовується, як правило, при здійсненні короткострокових фінансових операцій. Прикладами таких операцій є операції банків по наданню короткострокових позик та обліку векселів. Для визначення нарощеної суми за простими відсотками використовують наступну формулу:
де
Теперішню вартість грошей з використанням простих відсотків визначають за формулою, яка є оберненою до формули по визначенню майбутньої вартості грошей.
Визначаючи тривалість фінансової операції, день видачі та день погашення позики прийнято вважати за 1 день. Можливі 3 наступні варіанти нарахування відсотків: 1) звичайні відсотки з точною кількістю днів позики (французька практика); 2) звичайні відсотки з наближеною кількістю днів (німецька практика); 3) точні відсотки з точною кількістю днів позики (англійська практика). Звичайні (комерційні) відсотки визначаються виходячи з наближеної кількості днів у році, кварталі, місяці (відповідно 360, 90, 30). Точні відсотки враховують точну кількість днів у році (365 або 366), у кварталі (від 89 до 92), в місяці (від 28 до 31). Наближена кількість днів позики випливає з тривалості місяця в 30 днів.
Облік векселів банками – наступна операція, яка передбачає застосування простих відсотків. В цьому випадку мова йде про прості облікові ставки відсотків. Облік векселів - форма кредитування банком векселеотримувача шляхом дострокової виплати визначеної у векселі суми за мінусом певних відсотків. В даному випадку банком застосовується не математичне, а банківське дисконтування. Відповідно до цього методу відсотки за користування позикою нараховуються на суму, яка підлягає сплаті в кінці терміну повернення позики (сума по векселю, яку має сплатити боржник в кінці терміну його погашення). Ставка, на основі якої нараховуються відсотки, називається дисконтною ставкою (
Розрахунок наданої банком суми по векселю здійснюється за наступною формулою:
де
Операція дисконтування за обліковими ставками може поєднуватися з нарахуванням відсотків (i) за векселем. В цьому випадку сума, яка виплачуватиметься при обліку векселів, складає:
де Довгострокові фінансові операції (інвестування, кредитування та ін.), як правило, базуються на складних відсотках. Майбутня вартість грошей, розрахована з урахуванням складних відсотків, визначається за формулою:
де
Якщо передбачається, що нарахування відсотків здійснюється частіше, ніж один раз у рік, формула майбутньої вартості коригується таким чином, що річна ставка відсотку ділиться на кількість періодів в році, а кількість років множиться на кількість періодів у році. Ця процедура називається нарахуванням проміжного складного відсотку.
де Розрахувати майбутню вартість грошей можна також, використовуючи спеціальні таблиці факторів нарахування відсотків. Фактори нарахування показують суму, до якої виріс би початковий внесок в 1 грошову одиницю при різних комбінаціях періодів та відсоткових ставок. Так, одна грошова одиниця, покладена на депозит під 8% річних, через 2 роки зросте на 1.166 грошову одиницю. Використовуючи фактор нарахування відсотків для ставки 8% і 2 років (1.166), майбутню вартість інвестицій можна визначити, перемноживши інвестовану суму на відповідний фактор нарахування. Формула по визначенню майбутньої вартості грошей за складними відсотками з використанням таблиць факторних множників можна представити таким чином:
FM 1 (i;n) – мультиплікований множник для одиничного платежу; показує, чому буде дорівнювати 1 грошова одиниця через n періодів за заданої ставки i.
Різні фінансові контракти можуть передбачати різні схеми нарахування відсотків. Щоб забезпечити порівняльний аналіз ефективності таких контрактів, у фінансово-економічних розрахунках застосовується ефективна річна ставка відсотку
У фінансовій практиці часто стикаються із завданням, яке є зворотним до визначення майбутньої вартості грошей. Найчастіше це відбувається, коли необхідно визначити величину одноразового внеску, який забезпечить отримання певної суми в майбутньому; коли необхідно визначити максимальну ціну купівлі певного активу виходячи з доходів, які очікується отримати від нього в майбутньому. Теперішня вартість грошей визначається за наступною формулою:
FM 2 (i;n) – дисконтний множник для одиничного платежу; показує, чому буде дорівнювати з позиції поточного моменту одна грошова одиниця, яка перебуває в обігу n-періодів за заданої відсоткової ставки i.
Більшість сучасних фінансових операцій передбачають не разові платежі, а послідовність грошових надходжень або виплат протягом певного періоду часу. Прикладами таких операцій є отримання та погашення довгострокового кредиту, виплати відсотків по облігаціях, здійснення внесків у різні фонди тощо. Послідовний ряд виплат називають потоком платежів. Ряд послідовних платежів, що виплачуються або надходять через рівні проміжки часу, називають ануїтетом, або фінансовою рентою. Ануїтети класифікуються за такими ознаками: Ø величиною кожного окремого платежу – постійні (з рівними платежами) і змінні (з нерівними платежами); Ø інтервалом ануїтету (інтервал часу між послідовними платежами); Ø терміном ануїтету – строкові та безстрокові (вічні); Ø відсотковою ставкою (ставка, яка застосовується при нарахуванні або дисконтуванні ануїтетних платежів); Ø моментом виплати – звичайні (постнумерандо), що здійснюються в кінці відповідних періодів, та авансові (пренумерандо), що здійснюються на початку періодів. Оцінку вартості ануїтетних платежів можна здійснювати з позиції майбутнього і теперішнього моментів. В даному випадку йдеться про визначення майбутньої та теперішньої вартості ануїтету (з рівними платежами). Причому залежно від моменту здійснення платежів (в кінці або на початку року) визначення майбутньої і теперішньої вартості грошей має свої особливості. Необхідність обчислення майбутньої вартості ануїтету виникає тоді, коли необхідно визначити суму, яка сформується на рахунку при регулярному рівномірному вкладанні грошових коштів за певної ставки відсотку. Формула по визначенню майбутньої вартості звичайного ануїтету має наступний вигляд:
Відповідно до цієї формули, кожний внесок, крім останнього, приносить дохід (складні відсотки) з моменту депонування до моменту отримання кінцевої суми. Таким чином, сума, яка сформується на рахунку в кінці періоду, буде складатися із внесків, а також відсотків, що нараховуються на кожний з внесків, за винятком останнього. Визначити майбутню вартість ануїтету можна також з допомогою таблиць
де FM 3 (i;n) – множник нарощування для ануїтету; показує чому дорівнюватиме сумарна величина строкового ануїтету в 1 грошову одиницю до кінця терміну його дії (передбачається нарахування грошових коштів, а вилучення здійснюється по закінченні ануїтету). Для авансового ануїтету, тобто при депонуванні сум на початку кожного періоду, майбутня вартість грошових потоків визначається за формулою:
Визначення теперішньої вартості ануїтету дає змогу вирішити наступні питання: 1) за яку ціну може бути придбаний актив, який приноситиме певний рівномірний дохід протягом визначеного періоду часу; 2) якою повинна бути сума початкового внеску, який необхідно зробити для систематичного отримання в кінці кожного періоду протягом певної кількості років визначеної суми. Формула для обчислення поточної вартості звичайного ануїтету має наступний вигляд:
У випадку використання таблиць факторних множників формула по визначенню поточної вартості звичайного ануїтету записується так:
де FM 4 (i;n) – дисконтний множник ануїтету; показує, чому дорівнюватиме з позиції поточного моменту величина ануїтету з регулярними грошовими надходженнями в розмірі 1 грошова одиниця, який триває n рівних періодів із заданою ставкою i. Для визначення поточної вартості авансового ануїтету слід враховувати, що оскільки перший платіж здійснюється негайно, тобто в момент часу 0, першу суму дисконтувати не потрібно. Другий платіж за визначенням ануїтету здійснюється через один часовий інтервал. Отже, для визначення його поточної вартості дану суму необхідно перемножити на коефіцієнт дисконтування
Одним з поширених типів ануїтету є безстроковий ануїтет (довічна рента). Безстроковий ануїтет – це ануїтет, грошові надходження якого надходять достатньо тривалий час з певною періодичністю. Прикладами такого ануїтету є дивіденди за привілейованими акціями, англійські безстрокові державні облігації (консоль) та ін. Майбутню вартість такого ануїтету визначити неможливо, оскільки вона не є кінцевою величиною. Однак можна визначити теперішню вартість безстрокового ануїтету, скориставшись наступними формулами: 1) для звичайного ануїтету
2) для авансового ануїтету
Особливий випадок ануїтету – інвестиція з необмеженим строком життя, але з постійно зростаючою величиною річного доходу. Якщо такий ріст відбувається з темпом g, тоді поточна вартість такої “вічної інвестиції” можна визначити за формулою:
де g – темп приросту дивідендів (%).
Інфляція є об’єктивним, постійно діючим явищем, яке існує у всіх країнах з розвиненою економікою. В сучасній економічній теорії навіть прийнято вважати, що ріст рівня цін у межах 10% за рік є нормальним економічним явищем, яке стимулює розвиток виробництва. Концепція врахування фактора інфляції в інвестиційних розрахунках полягає в необхідності реального відображення вартості активів і грошових потоків, що генерує проект або фінансова операція. Методичний інструментарій прогнозування річного темпу та індексу інфляції базується на очікуваних середньомісячних її темпах. Для прогнозування річного темпу інфляції (ТІр) застосовується така формула: ТІр = (1+ТІм)12 – 1, (2.14) де ТІм – очікуваний середньомісячний темп інфляції у наступному періоді, виражений десятковим дробом. Річний індекс інфляції можна спрогнозувати, застосовуючи такі формули: ІІр = 1+ТІр або ІІр = (1+ТІм)12 (2.15) Методичний інструментарій формування реальної процентної ставки з урахуванням фактора інфляції базується на прогнозованому номінальному її рівні на фінансовому ринку і результатах прогнозу темпів інфляції. В основі розрахунку реальної процентної ставки з урахуванням фактора інфляції лежить модель В основному ризики поділяються на дві групи. До першої групи належать статистичні ризики. Це такі ризики, що можуть викликати втрати, відображені в балансі по завершенні окремого періоду роботи підприємства. До числа основних розрахункових показників оцінки належать: а) Рівень фінансового ризику. Його можна розрахувати за формулою:
де Рр- рівень фінансового ризику; Рт - можливість виникнення фінансового ризику; Рв- розмір можливих фінансових втрат при реалізації ризику. Як правило, розмір можливих фінансових втрат виражається абсолютною величиною, а імовірність їх виникнення - відповідними коефіцієнтами імовірності (коефіцієнтом варіації, бета-коефіцієнтом та ін.). б) Дисперсія. Враховує ступінь коливальності досліджуваного показника стосовно його середньої величини. Розраховується за формулою:
де <г - дисперсія; Я, - конкретне значення можливих варіантів очікуваного доходу за аналізованою фінансовою операцією; д- середнє очікуване значення доходу за аналізованою фінансовою операцією; Р - можливість одержання окремих варіантів очікуваного доходу за фінансовою операцією; л - число спостережень. в) Середньоквадратичне відхилення. Цей показник розраховується в такий спосіб:
де сг- середньоквадратичне відхилення; Я - конкретне значення можливих варіантів очікуваного доходу за аналізованою фінансовою операцією; Я~ середнє очікуване значення доходу за аналізованою фінансовою операцією; Р. - імовірність одержання окремих варіантів очікуваного доходу за фінансовою операцією; п - число спостережень. г) Коефіцієнт варіації. Він дозволяє визначити рівень ризику, якщо показники середнього очікуваного доходу від здійснення фінансових операцій різняться між собою. Коефіцієнт варіації розраховується за формулою:
де СУ - коефіцієнт варіації; а- середньоквадратичне відхилення; середнє очікуване значення доходу за аналізованою фінансовою операцією. д) Бета-коефіцієнт. Цей показник дозволяє оцінити індивідуальний і портфельний систематичний фінансовий ризик стосовно рівня фінансового ризику в цілому. Розрахунок проводиться за формулою:
де /?- бета-коефіцієнт; К-ступінь кореляції між рівнем доходності за окремим видом цінних паперів і середнім рівнем доходності даної групи фондових інструментів на ринку в цілому; а- середньоквадратичне відхилення доходності за окремим видом цінних паперів; а - середньоквадратичне відхилення доходності по фондовому ринку в цілому. Для оцінки рівня фінансового ризику окремих цінних паперів використовуються такі значення бета-коефіцієнтів: /?= 1 - середній рівень; Р> 1 - високий рівень; р< 1 - низький рівень. До другої групи належать динамічні ризики, тобто можливі втрати або витрати, викликані змінами в зовнішньому для підприємства середовищі. Ці зміни обумовлені головним чином економічним і соціально-політичним курсом країни в цілому. Встановлено, що аналіз фінансово-господарської діяльності підприємства з оцінкою її результатів повинен проводитися з урахуванням ризику і невизначеності. Існує різниця між ризиком і невизначеністю. Як правило, ризик проявляється в будь-якій діяльності підприємства, а невизначеність присутня тільки у випадках, коли наслідки управлінських рішень необхідно прогнозувати суб'єктивно. У зв'язку з цим завдання фінансистів-аналітиків полягають у такому: - виявлення факторів ризику внаслідок невизначеності інформації з реалізації фінансових рішень; - розрахунок інших можливих варіантів реалізації фінансових рішень, що мають негативні відхилення від базисного варіанта щодо різноманітних виявлених факторів ризику; - розробка методів організаційно-технічного характеру в складі проектних рішень, що дозволяють врахувати потенційну можливість появи негативних ситуацій і знизити або усунути їх негативні наслідки для фінансових рішень. Виявлення ризиків та їх врахування є частиною загальної системи фінансової надійності господарюючого суб'єкта. Крім урахування ризику надійності діяльність підприємства оцінюється рівнями її доходності І фінансової стійкості. При цьому має забезпечуватися мінімізація витрат і максимізація фінансової стійкості.
|


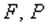 – відповідно майбутня і теперішня вартість грошових потоків;
– відповідно майбутня і теперішня вартість грошових потоків;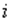 – річна ставка простих відсотків, виражена десятковим дробом;
– річна ставка простих відсотків, виражена десятковим дробом; – тривалість фінансової операції в днях;
– тривалість фінансової операції в днях; – розрахункова кількість днів в році.
– розрахункова кількість днів в році.
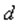 ). Чим вище значення цієї ставки, тим більшу суму банк утримує на свою користь.
). Чим вище значення цієї ставки, тим більшу суму банк утримує на свою користь.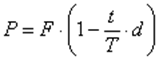
 - сума векселя;
- сума векселя; - приведена сума або вартість векселя (сума, що виплачується при обліку векселів);
- приведена сума або вартість векселя (сума, що виплачується при обліку векселів);
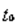 - термін нарахування відсотків.
- термін нарахування відсотків.
 - кількість років.
- кількість років.
 - кількість періодів нарахування відсотків в одному році.
- кількість періодів нарахування відсотків в одному році.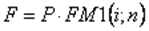 ,
, , яка розраховується наступним чином:
, яка розраховується наступним чином:
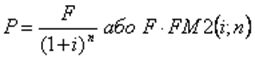

 факторних множників ануїтетних платежів.
факторних множників ануїтетних платежів.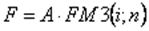 ,
, або
або

 ,
, для кінця першого періоду і т. д.
для кінця першого періоду і т. д.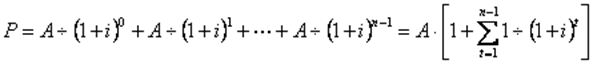 або
або


 ,
,







