ПАРАМЕТРЫ СТАТИСТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ
Математическое ожидание (среднее значение) EX случайной величины X. Представляет собой интеграл вида:
Для непрерывной случайной величины может быть выражено также через плотность ее распределения:
а для дискретной случайной величины - через функцию вероятности:
Дисперсия также называется рассеяние случайной величины X, имеет вид:
В классических методах теории риска дисперсия часто использовалась в качестве меры риска, измерителя рискованности проектов.
Стандартное отклонение случайной величины X задается выражением
Асимметрия распределения случайной величины X:
характеризует различие "хвостов" распределения. Асимметрия положительна при более тяжелом правом хвосте, и отрицательна при более тяжелом левом хвосте. Для симметричных распределений асимметрия равна нулю. Островершинность (эксцесс) распределения случайной величины X:
характеризует тяжесть "хвостов" распределения. Положительные значения этого параметра соответствуют распределениям с более тяжелыми хвостами, чем у нормального распределения.
Медианой a = med(X) распределения случайной величины X называется корень уравнения:
Медиана является средней характеристикой распределения в том смысле, что X с равными вероятностями принимает значения, лежащие справа и слева от a. Преимуществом медианы перед математическим ожиданием является тот факт, что математическое ожидание может быть неопределенным, если задающий его интеграл (в дискретном случае - ряд) расходится, как, например, в случае распределения Коши. Недостатком медианы является ее возможная неоднозначность для дискретных распределений. Медиана симметричного распределения совпадает с его средним значением (если последнее существует). Модой распределения называется наиболее вероятное значение случайной величины: в непрерывном случае - точка максимума плотности распределения, в дискретном случае - точка максимума функции вероятности. Мода распределения может быть неоднозначной, и использование этого параметра в теории риска ограничено.
|

 .
. ,
, .
. .
. .
. .
. .
.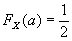 .
.


