Тема 3.4. Обыкновенные дифференциальные уравнения.
Цель:отработать навыки решения дифференциальных уравнений первого и второго порядка. Форма работы: решение задач. Задания для самостоятельной работы: 1.Решить дифференциальные уравнения первого порядка с разделяющимися переменными: 1) 2) 2. Решить линейные дифференциальные уравнения первого порядка: 1) 5.Решить задачу, приводящую к уравнению с разделяющимися переменными: Пусть жидкость вытекает из некоторого сосуда через отверстие в нем со скоростью, равной (Указание: с одной стороны объем вытекшей воды dvравенобъему цилиндрического слоя с высотой dh и радиусомR основания бака, т.е. dv=-πR2dh; с другой стороны, этот объем равен объему цилиндра, основанием которого служит отверстие в дне резервуара, а высота равна υdt,dv=0,6πr2
Список рекомендуемой литературы: 1. Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki 2. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.: Наука, 2004. 3. Данко П.Е., Попов А.Г., Коженикова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. – М.: Высшая школа, 1999. 4. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001. Порядок проверки, защиты самостоятельной работы: проверка рабочей тетради
|
;
;
;
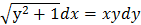, h – высота уровня жидкости над отверстием, g = 9,8 м/с2. За какое время вся жидкость вытечет из цилиндрического бака с диаметром 2R = 1,8м и высотой H=2,45м через отверстие в дне радиусом r=3см? Ось цилиндра вертикальная.
dt.Для составления уравнения необходимо приравнять получившиеся выражения)
