Жарықтың электромагниттік табиғаты
Максвелл теңдеулері. Электр зарядтарымен, электр тогымен және магниттермен жүргізілген тәжірибелерде алынған деректерді қорытындылау арқылы 19 ғ. екінші жартысында Максвелл (1831-1879) электромагниттік өрістер үшін теңдеулер жүйесін қорытып шығарды. Кейіннен жүргізілген зерттеулер Максвелл теңдеулерінің осы теңдеулерді алуға негіз болған деректер мен түсініктер шеңберінен әлдеқайда кең, өте терең физикалық мазмұны бар екендігін көрсетті. Бұл теңдеулер релятивтік инварианттылық шартын қанағаттандырады, тез өзгеретін, айнымалы электромагниттік өрісті, соның ішінде жарық толқындарын да, жақсы бейнелейді, қозғалыстағы зарядтардың электромагниттік толқындарды шығару теориясы және жарық пен заттың әсерлесу теориясы негізіне алуға болатындығы белгілі болды. Максвелл теңдеулерінен негізінде жаңа физикалық құбылыстың болатындығы жайында маңызды қорытынды шығады: электр зарядтарынсыз және электр тогынсыз да электромагниттік өріс өздігінше, дербес болуға қабылетті. Осы жағдайда электромагниттік өріс күйінің өзгеруі (өрістің ұйытқуы) міндетті түрде толқындық сипатта болады. Осындай өрістер электромагниттік толқындар деп аталады. Вакуумда мұндай толқындар 1. Айнымалы электромагниттік өріс кеңістікте бір орында тұрмайды, барлық жаққа 2. Электромагниттік толқын-көлденең толқын, яғни электр және магнит өрістерінің кернеуліктерінің векторлары толқынның таралу бағытына перпендикуляр: 3. Жазық электромагниттік толқында электр өрісінің кернеулік векторы мен магнит өрісі кернеулік векторының бағыттары бір-біріне өзара перпендикуляр, сонымен қабат олар электромагниттік толқынның таралу бағытына да перпендикуляр; және 4.
 және және  векторлары бірдей фазада тербеледі, яғни олар кеңістіктің бірдей нүктелерінде максимум немесе минимум мәндеріне бір мезгілде жетеді, яғни бұлар кеңістіктің берілген нүктесінде өздерінің максимум мәндеріне бір мезгілде жетеді және бір мезгілде нөлге айналады. векторлары бірдей фазада тербеледі, яғни олар кеңістіктің бірдей нүктелерінде максимум немесе минимум мәндеріне бір мезгілде жетеді, яғни бұлар кеңістіктің берілген нүктесінде өздерінің максимум мәндеріне бір мезгілде жетеді және бір мезгілде нөлге айналады.
Ток күшінің электромагниттік бірлігінің оның электростатикалық бірлігіне қатынасының вакуумдағы жарықтың жылдамдығына тең болуына сүйеніп Максвелл жарық-толқын ұзындығы қысқа электромагниттік толқын деген қорытынды жасады. Жарықтың бостықтағы жылдамдығының берілген ортадағы жарықтың фазалық жылдамдығына қатынасы ретінде анықталатын сыну көрсеткіші жарықтың электромагниттік теориясына сәйкес диэлектрлік тұрақтының магниттік өтімділікке көбейтіндісінің квадраттық түбіріне тең болады, яғни
Максвеллдің болжамдары кейіннен теориялық жолмен де, эксперименттік зерттеулер арқылы да расталды. Сөйтіп, жарық толқыны электромагниттік толқынның жоғарыда аталған барлық қасиеттеріне ие болатындығы анықталды. Енді электромагниттік толқынның аталған қасиеттерінің дәлелденуін келтірейік. Алайда мұны істемес бұрын осы процесс шынымен толқындық екендігін дәлелдеу керек. Дәлелдеу үшін толқындық теңдеуді қорытып шығару жеткілікті болады. Сонымен, электромагниттік толқында электр және магнит векторлары бірдей фазада (
Диэлектрик үшін Еркін электромагниттік толқында Электромагниттік толқын энергиясы. Умов-Пойнтинг векторы. Электромагниттік толқын таралған кезде энергия тасымалданады. Қайсыбір бет арқылы бірлік уақытта толқын тасымалдайтын энергия мөлшері энергия ағыны деп аталады және ол Ваттпен өлшенеді. Кеңістіктің әртүрлі нүктелеріндегі энергия ағысын сипаттау үшін энергия ағынының тығыздығы деп аталатын векторлық шама енгізіледі. Бұл шама берілген нүктеге энергияның тасымалдану бағытына перпендикуляр орналастырылған бірлік аудан арқылы өтетін энергия ағынына сан жағынан тең. Энергия ағыны тығыздығы векторының бағыты энергияның тасымалдану бағытымен дәл келеді. Энергия ағыны тығыздығының
мұндағы Кейіннен (1884 ж) осындай векторды электромагниттік толқындар үшін ағылшын физигі Пойнтинг (1852-1914) енгізген болатын. Осы себепті энергия ағыны тығыздығының векторы әдетте Умов-Пойнтинг векторы деп аталады. Сонымен энергия ағыны тығыздығын формула көмегімен
Берілген ортада
мұндағы
 (10.7) (10.7)
Фотометриялық шамалар. Бұлар энергетикалық шамаларға ұқсас, бірақ негізгі шама ретінде жарық күші алынады. Жарық күшінің бірлігі-кандела қара сәуле шығарғыш көмегімен анықталады; қара сәуле шығарғыш платинаның қату температурасы жағдайында істейтін негізгі эталон ретінде қабылданған. Бұл эталон 1967 ж. өлшемдер және таразылар бойынша ХIII Бас конференция шешімімен бекітілген. Жарық ағыны. Жарық ағыны деп жарық көзінің
Жарықтылық (яркость). Ол энергетикалық жарықтылық анықтамасына ұқсас енгізіледі а) б) Мысал ретінде кейбір жарық көздерінің жарықтылық мәндерін келтіреміз: айсыз түнгі аспан Жарқырау (светимость). Жарықталу (освещенность). жарықталу және жарықталудың спектрлік тығыздығы мына қатынастармен анықталады
Жарық экспозициясы. Бұл шама мына формуламен анықталады
мұндағы
|

 жарық жылдамдығына тең жылдамдықпен таралады.
жарық жылдамдығына тең жылдамдықпен таралады. жылдамдықпен электромагниттік толқын түрінде таралады, мұндағы
жылдамдықпен электромагниттік толқын түрінде таралады, мұндағы 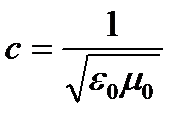 -вакуумдағы жарық жылдамдығы (
-вакуумдағы жарық жылдамдығы ( ).
). және
және  , мұндағы
, мұндағы  -берілген ортадағы толқынның таралу жылдамдығы.
-берілген ортадағы толқынның таралу жылдамдығы.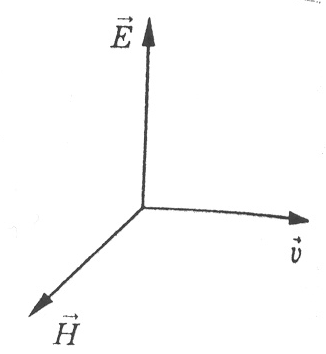
 .(10.1)
.(10.1)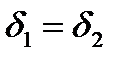 ) тербеліс жасайды, ал осы векторлардың амплитудалары мына қатынаспен байланысқан
) тербеліс жасайды, ал осы векторлардың амплитудалары мына қатынаспен байланысқан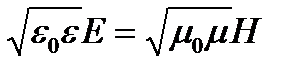 (10.2)
(10.2) , демек
, демек  . Вакуум үшін
. Вакуум үшін  және
және  .
. және
және  векторлары бір фазада тербеліс жасайды, яғни максимум немесе минимум мәндеріне бұлар кеңістіктің бірдей нүктелерінде және бір мезгілде жетеді.
векторлары бір фазада тербеліс жасайды, яғни максимум немесе минимум мәндеріне бұлар кеңістіктің бірдей нүктелерінде және бір мезгілде жетеді. векторын серпімді толқындар үшін 1874ж. қарастыруға алғаш енгізген Н.А.Умов (1846-1915). Ол кез-келген ортадағы энергия ағыны жайындағы жалпы теореманы дәлелдеді, Умов векторы мынаған тең
векторын серпімді толқындар үшін 1874ж. қарастыруға алғаш енгізген Н.А.Умов (1846-1915). Ол кез-келген ортадағы энергия ағыны жайындағы жалпы теореманы дәлелдеді, Умов векторы мынаған тең (10.3)
(10.3) -энергия тығыздығы;
-энергия тығыздығы;  -толқынның фазалық жылдамдық векторы, ол толқынның таралу бағытымен (энергияның тасымалдану бағытымен де) дәл келеді.
-толқынның фазалық жылдамдық векторы, ол толқынның таралу бағытымен (энергияның тасымалдану бағытымен де) дәл келеді. толқын жылдамдығына көбейтіндісі ретінде табуға болады. Өтімділіктері
толқын жылдамдығына көбейтіндісі ретінде табуға болады. Өтімділіктері 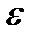 және
және 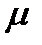 кәдімгі изотроп ортада электромагниттік өріс энергиясының тығыздығы электр және магнит өрістері энергиялары тығыздықтарының қосындысына тең:
кәдімгі изотроп ортада электромагниттік өріс энергиясының тығыздығы электр және магнит өрістері энергиялары тығыздықтарының қосындысына тең: (10.4)
(10.4) және
және 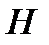 арасындағы қатынас орындалады, ал бұл қума толқындағы электр энергиясының тығыздығы магниттік энергия тығыздығына тең болатындығын білдіреді. Сондықтан өрнекті былай жазуға болады
арасындағы қатынас орындалады, ал бұл қума толқындағы электр энергиясының тығыздығы магниттік энергия тығыздығына тең болатындығын білдіреді. Сондықтан өрнекті былай жазуға болады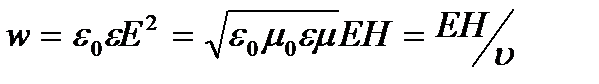 (10.5)
(10.5) (10.6)
(10.6) векторының бағыты энергияның тасымалдану бағытымен дәл келеді, ал осы вектордың модулі
векторының бағыты энергияның тасымалдану бағытымен дәл келеді, ал осы вектордың модулі  -қа тең. Сондықтан электромагниттік энергия ағыны тығыздығының
-қа тең. Сондықтан электромагниттік энергия ағыны тығыздығының  векторын мына түрде жазуға болады:
векторын мына түрде жазуға болады:
 жарық күшінің, ішінде шығарылған жарық таралатын
жарық күшінің, ішінде шығарылған жарық таралатын  денелік бұрышқа көбейтіндісін айтады
денелік бұрышқа көбейтіндісін айтады (10.8)
(10.8) ,
,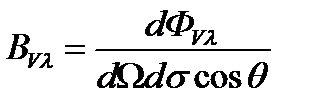 (10.9)
(10.9)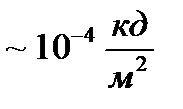 , толық ай-
, толық ай-  , бұлтсыз ашық күндізгі аспан-
, бұлтсыз ашық күндізгі аспан- 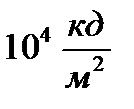 , Күн-
, Күн-  .
. (10.10)
(10.10) ,
,  ,(10.11)
,(10.11) (10.12)
(10.12) -уақыт аралығы, осы уақыт аралығы ішінде
-уақыт аралығы, осы уақыт аралығы ішінде 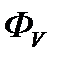 жарық ағыны шығарылады немесе қабылданады.
жарық ағыны шығарылады немесе қабылданады.


