Оценка случайной погрешностиДля того, чтобы оценить величину случайной погрешности, один и тот же опыт(измерение) необходимо повторить несколько раз. Пусть производится измерение некоторой физической величины x. При этом все составляющие погрешности за исключением случайной отсутствуют. Одно и то же измерение повторили n раз. Представим результат i-ого из этих n измерений как: xi = xи +Δxi, (7.1) где xи - истинное значение измеряемой физической величины, Δxi – абсолютная погрешность i-ого измерения(может быть, как со знаком «+», так и со знаком «-»). Для данного случая Δxi – случайная погрешность i-ого измерения. Определим сумму результатов измерения:
Поделим левую и правую части выражения (7.2) на n:
Левая часть выражения (7.3) есть не что иное, как среднее значение результатов n измерений. Обозначим его, как Из выражения (7.3) следует, что при увеличении количества измерений n случайная погрешность этих измерений уменьшается, а среднее значение Следует отметить, может сложиться впечатление, имея примитивную аппаратуру(измерительное средство) и наращивая количество измерений можно достичь достоверных результатов. Это не так: при росте числа измерений уменьшается только случайная погрешность, а остальные(инструментальная и методическая) остаются неизменными и определяют конечную точность измерений. На практике для оценки случайной погрешности обычно ограничиваются 5-10 измерениями. Рассмотрим числовую ось (рисунок 2.), на которой поместим среднее значение
X
Рисунок 2.- Числовая ось. Интервал 2Δx называется доверительным интервалом, внутри которого может оказаться истинное значение измеряемой физической величины. Следует отметить, что доверительный интервал не полностью характеризует точность выполненных измерений. Нужна ещё количественная оценка степени достоверности нахождения истинного значения xист измеряемой физической величины в пределах интервала 2Δx. В качестве такой характеристики используется доверительная вероятность P, под которой понимают вероятность нахождения xист в данном доверительном интервале. При этом, чем уже интервал, в котором предположительно находится измеряемая величина, тем меньше вероятность найти её в нём. Доверительная вероятность P, определяется как: P = где n - общее число выполненных измерений, n1 – число результатов измерений, попавших в доверительный интервал 2Δx. Выражение (7.4) не имеет практического применения, но хорошо поясняет суть понятия. Ещё проще, в самом первом приближении, опуская предел(7.4), доверительную вероятность оценить как отношение n1/ n. Итак, при оценке случайной погрешности по серии измерений необходимо найти два параметра: доверительный интервал и доверительную вероятность. На практике, чаще всего, значение доверительной вероятности задаётся. А доверительный интервал(случайная погрешность) определяется для заданного значения доверительной вероятности. Типовые значения задаваемой доверительной вероятности: 0,683;0,95; 0,99. Существуют разные методы определения доверительного интервала, но наиболее широко применяемым является способ оценки доверительного интервала с помощью среднеквадратической погрешности, σ;. В результате многочисленных исследований было установлено, что доверительный интервал заполняется результатами измерений неравномерно: они группируются преимущественно около среднего значения. В большинстве случаев такое распределение результатов измерения относится к так называемому нормальному распределению или распределению Гаусса, которое описывается выражением: f(x) = где Из выражения (7.5) следует, что распределение Гаусса задаётся двумя параметрами: Рисунок 3 – Вид функции Гаусса. Если число отклонений от среднего значения всех результатов измерения (многочисленных измерений) конкретной физической величины поместить под кривую Гаусса, то, как видно на рисунке 4, 68,2% всех измерений расположится в доверительном интервале 2 σ;(на рисунке 4 μ=
Рисунок 4 – Измерения в доверительном интервале.
Среднеквадратическую погрешность однократного результата измерения можно определить по n измерениям как: σ1 = Среднеквадратическая погрешность среднего арифметического результатов n измерений определяется следующим образом: σ = Следует, однако, отметить: определить границы доверительного интервала с достаточной степенью достоверности, используя выражения (7.5, 7.6) и распределение Гаусса, можно только при условии, что одна и та же физическая величина измерялась не менее 30-50 раз. Это слишком много для практических измерений. Но эта проблема была решена, когда в 1908 г. учёный-статистик Уильям Сили Госсет(William Sealy Gosset), известный под псевдонимом «Стьюдент», показал, что статистический подход справедлив и при малом числе измерений. Для расчёта случайной погрешности(полуширины доверительного интервала) он ввёл специальный коэффициент(коэффициент Стьюдента), зависящий от доверительной вероятности и числа измерений. При этом случайная погрешность (полуширина доверительного интервала), Δxсл, определяется как: Δxсл, = t σ;, (7.7) где t – коэффициент Стьюдента, который можно определить из таблицы 7.1, зная значение доверительной вероятности, P, и количество измерений n. Таблица 2.- Коэффициенты Стьюдента.
Итак, мы разобрались с методикой оценки случайной погрешности. А далее переходим к методике оценки систематической погрешности.
|
= nxи + 
,(7.2)
= xи + 
,(7.3)
.
стремится к истинному значению измеряемой физической величины. Это - важное свойство случайной погрешности, которое широко используется в практических измерениях.
измеряемой величины, относительно которой отложим влево и вправо значение погрешности Δx.
, (7.4)
2/2 σ2],(7.5)
– отклонение результата измерения, x, от среднего значения результатов измерения, 
.
). При доверительном интервале, равном 6 σ;, внутри этого интервала окажется 99,7% всех измерений (доверительная вероятность равна 0,997). По этой причине полуширину доверительного интервала(6 σ;), 3σ;, называют предельной случайной погрешностью.
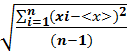(7.5)
(7.6)
