Пример 1.
В исследуемой электрической цепи на резисторе R1 сопротивлением =100 Ом, проводились измерения напряжения, U, с помощью цифрового вольтметра. Результаты многократных наблюдений представлены в таблице 3. Таблица 3 – Результаты многократных наблюдений.
Примечание: измеряемая физическая величина – напряжение, обозначается буквой u, а поэтому в формулах 10.1, 7.6, 7.7, 8.1, 9.1 x заменяется на u. Характеристики вольтметра: - входное сопротивление – Rv =10Мом; - приведённая погрешность, γ = 0,2%, - верхний предел диапазона измерений,Uв = 20 мВ, -относительная дополнительная погрешность, δдоп, описывается выражением: δдоп= 0,02%( Условия измерения:t = 120 С; доверительная вероятность P=0,95. Обработку результатов измерения проводим в соответствии с выше представленными рекомендациями (10): 1.Просмотрев результаты в таблице 3, исключаем результат под номером 3, как промах (сильно отличается от остальных результатов). 2. Анализируем методику измерения на предмет наличия исключаемых систематических погрешностей. Для нашего случая к ним можно отнести: погрешность, связанную с возможным смещением «нуля» вольтметра и погрешность взаимодействия, вызванную шунтированием резистора R1 входным сопротивлением вольтметра. Соединяем клеммы входного кабеля вольтметра между собой. Показания вольтметра: -0,35 мВ. Это – исключаемая систематическая погрешность. Исправляем результаты таблицы 11.1. Исправленные результаты представлены в таблице 4. Таблица 4 - Исправленные результаты.
Анализируем возможную погрешность взаимодействия исследуемого объекта (резистора R1, на котором измеряем напряжение) и вольтметра. Определим отношение параллельного соединения R1, Rv к R1:
Видим, что изменение сопротивления составляет всего 0,001%, что в 200 раз меньше приведённой погрешности вольтметра. Таким образом, вклад погрешности взаимодействия в полную погрешность ничтожен. Этой погрешностью можно пренебречь. 3.Вычисляем среднее арифметическое, ‹u›, исправленных результатов наблюдений. ‹u › =3,34 мВ 4.Вычисляем среднеквадратическую погрешность, σ;, результата измерения, используя выражение 7.6. σ;= 0,016мВ 5.Определяем из таблицы 7.1 для Р=0,95 и n=8 коэффициент Стьюдента. t= 2,365 6. Вычисляем случайную погрешность. Δuсл, = tσ = 0,038 мВ 7.Оценим значения неисключённых систематических погрешностей. Для нашего случая к этим погрешностям относятся: основная и дополнительная погрешности вольтметра. Рассчитываем абсолютное значение основной погрешности Δu1, используя значения приведённой погрешности, γ, и верхнего предела диапазона измерений, Uв. Δu1 = γ Uв/100% = (0,2%)20/100% =0,04[мВ] Рассчитываем абсолютное значение дополнительной погрешности, Δu2: Δu2 = δдоп Uв/100% = (0,05%)( 8.Вычисляем полную неисключённую систематическую погрешность, Δuсис= 1,1 9.Вычисляем с помощью выражения 9.1 полную погрешность, Δu, включающую в себя случайную и систематические погрешности. Δu = 10.Вычисляем относительную погрешность, δ. δ= 11.Записываем результат измерения: u= 3,34 δ=1,74%
|

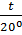 - 1), где t – температура окружающей среды.
- 1), где t – температура окружающей среды.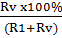 = 99,999%.
= 99,999%.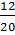 - 1)20/100% = -0,004[мВ]
- 1)20/100% = -0,004[мВ]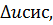 для заданного значения доверительной вероятности P=0,95по формуле 8. 1.
для заданного значения доверительной вероятности P=0,95по формуле 8. 1.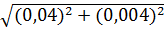 = 0,044[мВ]
= 0,044[мВ]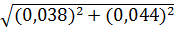 = 0,058[мВ]
= 0,058[мВ]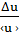 100% = 1,74%
100% = 1,74%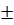 0,058[мВ] Для P=0,95
0,058[мВ] Для P=0,95


