Совместные измерения
Если некоторая физическая величина y зависит от другой величины, то эту зависимость можно установить, измеряя при различных значениях x. В результате измерений получается ряд значений: x1, x2,..., xi,,..., xn; y1, y2,..., yi,,..., yn. По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет метод наименьших квадратов, разработанный Ж.Лежандром ещё в 1806 г. Экспериментальные точки, как правило, не ложатся точно на кривую (рисунок 6). y 0 Рисунок 6 – Кривая экспериментальных точек. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. [yi – ƒ(xi)]2 была наименьшей. На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости (рисунок 7), т.е. когда y = kx или y = a + bx. (15.1)
Рисунок 7 – Линейная аппроксимация результатов измерения. Линейная зависимость очень широко распространена в разных областях науки и техники. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например: показатель преломления стекла n связан с длиной λ; световой волны соотношением n = a + b/λ2. При этом на графике строят зависимость n от λ-2. Мощность гармонического сигнала пропорциональна квадрату амплитуды сигнала и т.д. Возможен и другой подход – кусочно-линейная аппроксимация кривой, т.е.замена кривой отрезками прямых (рисунок 8). y
X
Рисунок 8 – Кусочно – линейная аппроксимация кривой.
Итак, чаще всего при совместных измерениях приходится иметь дело с линейными зависимостями или всё сводят к линейным зависимостям. На них и остановимся. Рассмотрим зависимость y = kx (прямая, проходящая через начало координат). Составим величину φ; – сумму квадратов отклонений наших точек от прямой
Величина φ; всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ;имеет минимум
Рассмотрим теперь несколько более трудный случай, когда точки должны удовлетворить формуле y = a + bx (прямая, не проходящая через начало координат). Задача состоит в том, чтобы по имеющемуся набору значений xi, yi найти наилучшие значения a и b. Снова составим квадратичную форму φ;, равную сумме квадратов отклонений точек xi, yi от прямой
и найдем значения a и b, при которых φ; имеет минимум из решения системы уравнений:
.Совместное решение этих уравнений даёт
Среднеквадратические погрешности определения a и b равны:
Следует отметить, что при совместных измерениях часто ограничиваются именно среднеквадратическими погрешностями. Но в отдельных случаях требуются более «жёсткие» вероятностные гарантии нахождения коэффициентов « a» и « b». Тогда их определяют с учётом доверительной вероятности, используя коэффициенты Стьюдента( t ). При этом результаты исследования записываются в виде: a Δb = tSb. При обработке результатов измерения этим методом удобно все данные сводить в таблицу, в которой предварительно подсчитываются все суммы, входящие в формулы (15.6)–(15.10). Формы этих таблиц приведены в рассматриваемом ниже примере. Пример. Вычислим температурный коэффициент сопротивления металла по методу наименьших квадратов. Сопротивление зависит от температуры по линейному закону Rt = R0(1 + α t°) = R0 + R0 α t°. Свободный член определяет сопротивление R0 при температуре 0° C, а угловой коэффициент – произведение температурного коэффициента α на сопротивление R0. Результаты измерений и расчетов приведены в таблице (см. таблицу 6). Таблица 6 – Результаты измерений и расчетов.
По формулам (15.7) определяем
R0 = ¯R- α R0¯ t = 1.4005 - 0.002645 · 85.83333 = 1.1735 Ом. Отсюда:
Найдем ошибку в определении α. Так как
Пользуясь формулами (15.8), (15.9) имеем
= 0.014126 Ом. Тогда
Задавшись надежностью P = 0.95, по таблице(7.1) коэффициентов Стьюдента для n = 6, находим t = 2.571 и определяем абсолютную ошибку Δα = 2.571 · 0.000132 = 0.000338 град-1. α = (23 ± 4) · 10-4 град -1 для P = 0.95.
|

 x
x

 . (15.2)
. (15.2) (15.3)
(15.3) (15.4)
(15.4) (15.5)
(15.5) ;(15.6)
;(15.6) .
.
 . (15.7)
. (15.7) (15.8)
(15.8) (15.9)
(15.9)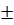 Δa; b
Δa; b  ,
, .
. , то по формуле (15.9) имеем:
, то по формуле (15.9) имеем: .
.
 ;
;
 .
. .
.


