Обработка результатов косвенных измерений
При косвенных измерениях значение искомой физической величины находят на основании известной функциональной зависимости между ней и величинами, подвергаемыми прямым измерениям. 12.1. Рассмотрим вначале простейший случай - искомая физическая величина y задана функцией одной переменной: y=f(x). Её график представлен на рисунке 12.1. Y K f(x) y2 y0 y1 ά; 0 X x1 x0 x2 Рисунок 5 – Физическая величина, заданная функцией одной переменной.
На рисунке 5: K - касательная к кривой f(x) в точке с координатами (x0;y0); x1=x0 - Δx; x2=x0+Δx; y1=y0-Δy; y2=y0+Δy. Анализируя рисунок 12.1, получаем: Δy= tg(ά)Δx. Но tg(ά) = Δy= Принимая во внимание выражение (12.1), обработку результатов измерения с многократными наблюдениями для функции одной переменной, осуществляем в следующем порядке: 1.По методике 10 обрабатываем результаты прямого измерения физической величины x,получаем: x= 2.Вычисляем
3. Используя выражение12.1, вычисляем Δy. 4.Вычисляем относительную погрешность δ = 5.Записываем конечный результат, как: y= δ=… 12.2 Рассмотрим более сложный случай: измеряемая величина y является функцией некоторого числа(m) измеренных величин xi: y= f(x1, x2,…xm) (12.3) Среднее значение Δy= где Δxi – полная абсолютная погрешность измерения физической величины xi,
Частная производная – это такая производная, которая вычисляется от функции f по аргументу xi при том, как все остальные аргументы считаются постоянными. А теперь на основании всего выше изложенного представим рекомендации по обработке результатов косвенных измерений.
|

 (в точке x=x0). С учётом этого:
(в точке x=x0). С учётом этого: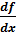 Δx (12.1)
Δx (12.1) Δx […] Для P = …
Δx […] Для P = … как:
как: =f(
=f(  (12.2)
(12.2) 100%
100%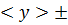 Δy […] Для P = …
Δy […] Для P = … определяется подстановкой
определяется подстановкой  i
i  в выражение (12.3). Полная абсолютная погрешность измерения величины y определяется по формуле:
в выражение (12.3). Полная абсолютная погрешность измерения величины y определяется по формуле: ,(12.4)
,(12.4) - обозначает так называемую частную производную.
- обозначает так называемую частную производную.


