Лабораторная работа № 25
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ВОЗДУХА, ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА, ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА
ОБОРУДОВАНИЕ: манометр жидкостный открытый, стеклянный сосуд со сливом внизу, капилляр, секундомер, мензурка для слива воды.
КРАТКИЕ ТЕОРИТИЧЕСКИЕ СВЕДЕНИЯ При движении слоев жидкости или газа с различными скоростями между ними действуют силы внутреннего трения или силы вязкости. Численное значение силы вязкости можно определить по формуле Ньютона:
η- коэффициент внутреннего трения или коэффициент динамической вязкости, S - площадь слоев.
Коэффициент динамической вязкости может быть выражен формулой:
т.е. он численно равен силе внутреннего трения, возникающей между двумя слоями жидкости и газа, имеющими площадь соприкосновения, равную единице, при градиенте скорости, равном единице. В системе СГС коэффициент динамической вязкости измеряется в Пуазах, в системе СИ - Н*сек/м2. С точки зрения молекулярно-кинетической теории коэффициент динамической вязкости численно равен количеству упорядоченного движения, переносимого за единицу времени через единицу площади соприкасающихся слоев при градиенте скорости, равном единице. Наряду с коэффициентом динамической вязкости часто употребляют коэффициент кинематической вязкости, определяемый следующим образом:
где р - плотность жидкости или газа. Для определения коэффициента динамической вязкости воспользуемся формулой Гагена-Пуазейля
Справедливой для случая установившегося ламинарного течения вязкой, несжимаемой жидкости по капилляру длинной l и радиусом r.
V'— объем жидкости. прошедшей через поперечное сечение капилляра в единицу времени. η- коэффициент динамической вязкости. Если разность давлений будет достаточно мала для того, чтобы можно было пренебрегать сжимаемостью газа, то формула (4) может быть применена к ламинарному течению воздуха через капилляр. Установить характер течения воздуха позволяет число Рейнольдса R
где ʋ - средняя скорость течения воздуха через капилляр
S=πr2 поперечное сечение капилляра 7 r - радиус капилляра, ρ - плотность воздуха. V - объём воздуха прошедшего через поперечное сечение капилляра. Для ламинарного течения требуется выполнение условия R < 1000. Объем воздуха V, протекающего через сечение капилляра за время t будет равен
Тогда для коэффициента динамической вязкости η легко получить
2. ОПРЕДЕЛЕНИЕ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ Для определения длины свободного побега молекул воспользуемся известным в молекулярной физике соотношением:
Где u - cредняя тепловая скорость молекул газа:
λ – средняя длина свободного побега молекул μ – молярная масса в-ва. ρ - плотность воздуха Плотность воздуха нетрудно выразить из уравнения Клайперона – Менделеева
P-давление идеального газа R-универсальная газовая постоянная R= 8,31 дж/моль к T абсолютная температура Объединив (10), (11), (12). получаем:
3. ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА
Средняя длинна свободного пробега может быть определена из выражения:
где σ- эффективный диаметр молекул, n- концентрация молекул газа. Концентрацию молекул воздуха при данной температуре можно выразить из хорошо известной формулы
Где k – постоянная Больцмана
Выразив σ после подстановки (15) в (14) получим:
Описание экспериментальной установки
рис.1 Лабораторная установка состоит из капилляра, водного манометра, сосуда с водой, вентиля, соединённых гибкими трубками (рис.1), и секундомера. Манометр позволяет измерить разность давлений воздуха (p2-p1) на концах капилляра в мм водного столба. Зная плотность воды разность давлений легко перевести в систему СИ: (p2-p1)=ρqh 17 ρ- плотность воды ρ= 1000кг/м3 q-ускорение свободного падения h-разность уровней воды в коленах манометра Вентиль позволяет регулировать скорость вытекания жидкости из сосуда и разность уровней жидкости в манометре. Сосуд (или пробирка для сбора воды) снабжён делениями позволяющими определить объём воздуха прошедшего через капилляр (равен объёму вытекшей воды). ХОД РАБОТЫ
1. Измерить давление воздуха в лаборатории с помощью барометра. 2. Измерить температуру в лаборатории с помощью термометра. 3. При закрытом вентиле наполнить сосуд водой до верхней отметки шкалы. 4. Осторожно регулируя вентилем скорость течения жидкости установить разность h уровней манометра 4-5 мм (занести h таблицу). 5. Измерить секундомером время вытекания 100 мл воды (объём задаётся преподавателем). 6. Повторить эксперимент с пункта 3 не менее трёх раз. 7. Занести данные измерений в таблицу и предъявить преподавателю на проверку. ЗАДАНИЯ
1. Используя известные параметры лабораторной установки и результаты измерений рассчитать по формуле (9) коэффициент динамической вязкости воздуха η. 2.Убедиться, что течение воздуха по капилляру носит ламинарный характер (рассчитать число Рейнольдса R по формуле 5, R < 1000). 3. Рассчитать по формуле (13) λ – среднюю длину свободного побега молекул воздуха. 4 Рассчитать по формуле (16) σ- эффективный диаметр молекул воздуха. 5 Рассчитать по методике прямых измерений погрешность измерений (методика расчёта погрешности может быть изменена преподавателем).
молярная масса воздуха μ =29 г/моль. длинна капилляра l =17,2 мм. радиус капилляра r=1,0 мм.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Явления переноса (диффузия, вязкость, теплопроводность) 2. Уравнения Фурье, Фика, Ньютона. Физический смысл коэффициентов переноса. ЛИТЕРАТУРА И..К. Кикоин, АХ. Кикоин Молекулярная физика»
[1] О классе точности приборов см.: Указания к выполнению лабораторных работ, ч. 2 «Электричество и магнетизм». [2] ГОСТ 8.207-76 устанавливает, что если D x сист < 0,8
[3] Строго говоря, погрешность результата измерения Δ х следует выражать одной или двумя значащими цифрами. Две цифры оставляют при наиболее точных измерениях, а также в тех случаях, когда цифра старшего разряда числа, выражающего погрешность, меньше или равна 3. 1 e - греч. «эпсилон» [4] Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).
1 За одно полное колебание тело проходит расстояние S =4A.
2 Момент инерции - скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями: J = Jc + ma2. 1 Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы). 2 См. лабораторную работу № 12. 1 Период простого колебания равен половине периода полного колебания. 1 Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы). [6] Градиент - мера возрастания или убывания в пространстве какой-л. физической величины при перемещении на единицу длины. Многие физические величины могут не только изменяться с течением времени, но и быть различными в разных точках пространства в один и тот же момент времени. Под «скоростью» понимают темп изменения физической величины во времени, а под «градиентом» — степень её изменения в пространстве. 1 Гомогенный - однородный по своему составу или происхождению. 2 Гетерогенный - состоящий из различных по составу, свойствам, происхождению частей. 1 Градиент – мера возрастания или убывания в пространстве какой-либо физической величины на единицу длины. 2 Триботехника – наука о контактном взаимодействии твердых тел при их относительном движении. 1 Другое определение: фаза — гомогенная часть гетерогенной системы. 1 Необходимо обратить внимание на слова “единственным результатом»; запреты второго начала снимаются, если процессы, о которых идет речь, не является единственными.
2 то есть каждому состоянию соответствует определённое значение энтропии. 3 Знаком d Q обозначено то, что количество теплоты не является полным дифференциалом, так как зависит не только от начального и конечного состояния системы, но и от пути перехода. 4 Флуктуация – случайное отклонение величины, характеризующей систему из большого числа частиц, от её среднего значения.
|

 (1)
(1) - градиент скорости.
- градиент скорости. (2)
(2) (3)
(3) 4
4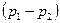 разность давлений на концах капилляра.
разность давлений на концах капилляра.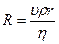 , 5
, 5 6
6 8
8 9
9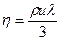 10
10 11
11 :
: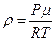 12
12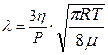 13
13 14
14
 15
15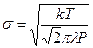 16
16
 , то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата в виде
, то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата в виде 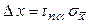 . Если D x сист > 0,8
. Если D x сист > 0,8 


