Прямая линия на плоскости
Общее уравнение прямой на плоскости: Ах + В у + С = 0. Уравнение прямой с угловым коэффициентом (рис. 3): у = k x + b. (6) Уравнение вертикальной прямой (рис. 3): х = а. (7)
у – y 0 = k (x – x 0). (8) Угловой коэффициент прямой, проходящей через две заданные точки А (х 1; у 1) и В (х 2; у 2):
Уравнение прямой, проходящей через две заданные точки:
Пусть на плоскости заданы две прямые, которым соответствуют уравнения с угловыми коэффициентами: у = k 1 x + b 1 и у = k 2 x + b 2. Условие параллельности прямых на плоскости: k 1 = k 2.. (11) Условие перпендикулярности прямых:
Если одна из двух перпендикулярных прямых вертикальная, т.е. k 2 не существует, то k 1 = 0 и обратно: если k 2 = 0, то k 1 не существует. Тангенс острого угла между пересекающимися прямыми можно найти, используя формулу:
откуда
Примерный вариант и образец выполнения контрольной работы по теме «Аналитическая геометрия» Задача 1. Даны координаты вершин треугольника АВС: А (–3; –1), В (4; 6), С (8; –2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. Задача 2. Даны координаты точки А (3; 0), уравнение прямой l: 3 x = 4 и число λ; = 3: 2. Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ;. Сделать чертеж в системе координат.
Решение задачи 1. 1) Вычислим длину стороны ВС по формуле (1): | BС |=
2) Составим уравнение стороны ВС, используя формулу (10):
3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (9):
и возьмем из уравнения ВС угловой коэффициент прямой ВС: Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (13) вычислим
4) Для получения уравнения высоты АK, проведенной из вершины А, используем уравнение пучка прямых (8) и условие перпендикулярности прямых (12). Сначала вычислим угловой коэффициент прямой АK. Так как Уравнение AK получим по формуле (8): у – уА = kAK (x – x A) x –2 y + 1 = 0 – уравнение AK.
5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если AМ – медиана треугольника и P – точка пересечения его медиан, то P делит AМ в отношении 2: 1, начиная от точки А, т.е. Основание медианы AМ – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3):
Теперь, когда координаты концов отрезка AМ известны, найдем координаты точки P, которая делит AМ в отношении
P (3; 1) – центр тяжести треугольника АВС.
6) Построим чертеж к задаче в системе координат ХОY (рис. 11). Полученные при решении задачи результаты не противоречат чертежу.
Ответы: 1) длина стороны | BС | = 2) уравнение стороны ВС: y = –2 x + 14; 3) угол при вершине В: 4) уравнение высоты АK: x –2 y + 1 = 0; 5) координаты центра тяжести треугольника P (3; 1); 6) чертеж на рис. 11.
Варианты контрольной работы по теме «Аналитическая геометрия» Каждый вариант КР содержит 4 задачи, охватывающих материал по теме «Аналитическая геометрия». Перед выполнением КР необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы. Задачи 1 и 3 являются частными случаями полностью разобранных задач 2 и 4. Cтуденту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление КР должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Варианты КР №1 ВАРИАНТ 1 1. Даны три вершины трапеции ( 2. Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3. Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 4. Заданы координаты точек– вершин пирамиды ABCD: А(6;5;8), В(3;5;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 2 1. Даны три вершины параллелограмма ABCD: А(-3,-2), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD.
ВАРИАНТ 3
1) Даны вершины треугольника: А(1,3), В(5, 1), С(-3,-1). Найти уравнение средней линии треугольника 2) Даны координаты вершин треугольника АВС: А(–3;–2), В(4;3),С(8;6). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Найти точку пересечения прямой L: 4) Заданы координаты точек–вершин пирамиды ABCD: А(4,10,9), В(5,7,4), С(5,2,6), Д(1,8,2). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол ВАРИАНТ 4
1) Даны три вершины параллелограмма: А(-4,1), В(-2, -1), С(2,-1). Найти уравнение и длину высоты, опущенной из вершины А на CD если 2) Даны координаты вершин треугольника АВС: А(1;–2), В(4;3),С(5;2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить уравнение плоскости, проходящей через точку K(2,3,-1) параллельно векторам 4) Даны 4 точки: М(2,0,-1), А(2,-1,1), В(0,-7,4), С(5,2,-2). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 5
1. Даны три вершины треугольника: А(-1, -3), В(4, 2), С(4,-4). Найти точку пересечения высоты треугольника Р и ее расстояние до АВ. 2. Даны координаты вершин треугольника АВС: А(1;–2), В(4;3),С(5;2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3. Составить геометрическое место точек, равноудаленных от плоскостей x+2y-2z-12=0 и 2x-y+2z-15=0. 4. Заданы координаты точек–вершин пирамиды ABCD: А(3,-1,2), B(4,-1,-1), C(2,0,2), А4(2,-1,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 6
1) Даны вершины треугольника А(1;3), В(5;1), С(-3;-1). Найти уравнение средней линии треугольника (МN // ВС) и расстояние от вершины А до этой линии МN. 2) Даны координаты вершин треугольника АВС: А(1;2), В(-4;3),С(5;-2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить уравнения прямой, проходящей через точку Р(4,-1,3) параллельно вектору 4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 7
1) Даны вершины треугольника: А(0,5), В(2,-4), С(-5,2). Найти точку пересечения высоты треугольника 2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить уравнения биссекторной плоскости, для данных плоскостей: x+ y + 5z + 1 = 0 и 5x-y+ z+4=0. 4) Заданы координаты точек–вершин пирамиды ABCD: А(0,2,2), B(-1,-2,3), C(4,5,-2), D(5;4;1). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 8 1) Даны уравнения сторон параллелограмма ABCD: АВ: x + y = 2, AD: y + 1 = 0 и точка пересечения его диагоналей Р(1,1). Найти уравнения диагоналей параллелограмма. 2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Найти проекцию точки А(2;5;1) на плоскость x+2y-3z-5=0. 4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол ВАРИАНТ 9 1) Даны 3 вершины трапеции А(-3;-3), В(-2;1), С(1;2). Найти уравнение основания АД(АД//ВС) и длину высоты, проведенной из вершины В. 2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Найти угол между прямой АВ и прямой 4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол ВАРИАНТ 10 1) Даны уравнения боковых сторон равнобедренного треугольника: АВ: x - y = 0, AС: x - 7y = 1 и точка пересечения медиан Р(2,0). Найти уравнение стороны ВС. 2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Найти угол между прямой АВ и плоскостью x-7y-2z+5=0, если А(1,9,2), В(5,1,4). 4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 11
1) Даны две вершины ромба: А(-1,-4), В(3,-1) и уравнение его диагонали BD: x + 2y - 1 = 0. Найти вершины ромба С и D. 2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить геометрическое место точек, равноудаленных от плоскостей x+2y-2z-18=0 и 2x-y+2z-15=0 4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,2), B(2,0,3), C(0,-1,2), D(2,3,4). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 12
1) Даны вершины треугольника: А(1,-1), В(-2,1), C(3,-5). Найти уравнение перпендикуляра, опущенного из точки пересечения медиан треугольника на его сторону АВ. 2) Даны координаты вершин треугольника АВС: А(3;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Вычислить расстояние между плоскостями x+2y-2y-6=0 и 2x+4y-4z-24=0. 4) Заданы координаты точек–вершин пирамиды ABCD: А(-1,1,3), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 13 1) Даны вершины треугольника А(1;3), В(5;1), С(-3;-1). Найти уравнение средней линии треугольника (МN // ВС) и расстояние от вершины А до этой линии МN. 2) Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 4) Заданы координаты точек– вершин пирамиды ABCD: А(-6;5;2), В(3;5;4), С(8;4;6), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол ВАРИАНТ 14 1) Даны две вершины ромба: А(-1,-5), В(3,-3) и уравнение его диагонали BD: x + 2y - 1 = 0. Найти вершины ромба С и D. 2) Даны координаты вершин треугольника АВС: А(–4;–1), В(4;5),С(8;–3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить параметрические уравнения прямой, проходящей через точку А(3;4;5) перпендикулярно векторам 4) Заданы координаты точек– вершин пирамиды ABCD: А(6;5;8), В(3;5;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
ВАРИАНТ 15 1) Даны уравнения боковых сторон равнобедренного треугольника: АВ: x - y = 0, AС: x - 7y = 1 и точка пересечения медиан Р(2,0). Найти уравнение стороны ВС. 2) Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 4) Заданы координаты точек– вершин пирамиды ABCD: А(6;5;8), В(3;5;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол ВАРИАНТ 16 1) Даны три вершины трапеции ( 2) Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат. 3) Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 4) Заданы координаты точек – вершин пирамиды ABCD: А(-2;-5;8), В(3;4;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол
Вопросы для самопроверки 1. Запишите формулу для вычисления расстояния между двумя точками 2. Запишитеобщее уравнение прямой на плоскости 3. Запишите уравнение прямой с угловым коэффициентом на плоскости 4. Запишите формулу для вычисления углового коэффициента прямой 5. Запишите уравнение прямой, проходящей через две заданные точки 6. Запишитеобщее уравнение плоскости 7. Запишите каноническое уравнение прямойв пространстве 8. Запишите формулу для вычисления угла между прямой и плоскостью Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с. 2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М.: Высш. шк., 1998.– 479 с.
|

 Уравнения прямых, проходящих через одну заданную точку М (х 0; у 0) (уравнение пучка прямых):
Уравнения прямых, проходящих через одну заданную точку М (х 0; у 0) (уравнение пучка прямых): . (9)
. (9)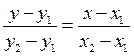 . (10)
. (10) . (12)
. (12) , (13)
, (13)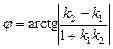 . Если одна из прямых вертикальная, т.е. k 2 не существует, то
. Если одна из прямых вертикальная, т.е. k 2 не существует, то  .
. =
= 

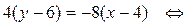
 y = –2 x + 14 – уравнение ВС.
y = –2 x + 14 – уравнение ВС.
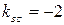 .
.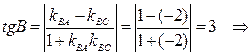
 .
. , то
, то  .
. у – (–1) =
у – (–1) =  (x – (–3))
(x – (–3)) 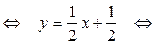
 .
.
 М (6; 2).
М (6; 2). = 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):
= 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):



 ;
;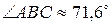 ;
; ): А(-3,-3), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD.
): А(-3,-3), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD. и
и  .
. между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол
между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол  между ребрами AB и BC; 8) найти угол
между ребрами AB и BC; 8) найти угол  между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.
между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.
 .
.
 и расстояние от вершины A до MN.
и расстояние от вершины A до MN. с плоскостью y + 5z + 1 = 0.
с плоскостью y + 5z + 1 = 0. .
. и
и  .
. между ребрами AB и BC; 8) найти угол
между ребрами AB и BC; 8) найти угол 
 между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол
между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол  между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.
между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.
 .
. и ее медианы СM.
и ее медианы СM. между ребрами AB и BC; 8) найти угол
между ребрами AB и BC; 8) найти угол  между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.
между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.
 , если А(4;8;0), В(7;8;2).
, если А(4;8;0), В(7;8;2).
 и
и  .
. и
и  .
. ): А(-3,-3), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD.
): А(-3,-3), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD. и
и 


