Детальная разбивка кривых
Рис. 9.16. Способ прямоугольных координат Кривая разбивается на равные части через k = 1; 5; 10; 20; … м. Для построения точек на местности по значению длины дуги k вычисляется угол Х1 = Rsinb, У1 = Х2 = Rsin2b, У2 = На местности для построения т. 1 отрезок Х1 откладывают от НК по линии тангенсов, по перпендикуляру - У1. Для построения т. 2 отрезок Х2 откладывают от НК по линии тангенсов, по перпендикуляру - У2. Более точно положение т. 1 получают откладыванием отрезка k по линии тангенсов и назад отступают на величину k – х1, т. 2 откладыванием отрезка 2 k по линии тангенсов и назад отступают на величину 2 k – х2 и т.д. 2. Способ продолженных хорд (в стесненных условиях при 200 £ R £300 м). Шаг разбивки кривой а. По значению а и радиусу R вычисляют координаты т. 1 по формулам (9.8) Для построения т. 1 (рис. 9.17) по линии тангенсов на местности откладывают от НК отрезок х1, а по перпендикуляру - у1. Для построения т. 2 соединяют НК, т. 1 и далее в створе откладывают отрезок а. Получают вспомогательную т. 2¢. Из т. 2¢ отрезком, равным b, а из т. 1 отрезком, равным а, получают т. 2. Для построения т. 3 соединяют т. 1, т. 2 и далее в створе откладывают отрезок а. Получают вспомогательную т.3¢. Из т. 3¢ отрезком, равным b, а из т. 2 отрезком, равным а, получают т. 3.
у1 =
Рис. 9.17. Способ продолженных хорд 3. Способ углов (в любых условиях, при любых R) Угол Для построения т. 1 (рис. 9.18) теодолитом от линии тангенсов строят угол
Рис. 9.18. Способ углов
Рис. 9.19. Вынос пикета на кривую От НК до пк 11 (рис. 9.19) вычисляют расстояние С учетом формулы b = а затем координаты выносимого пикета по формулам: х = R sinb, у = х = 500 м × sin 4°45¢20² = 41,45 м; У = 2∙ 500 sin2 2°22¢40² = 1,72 м. Для выноса пикета на кривую от пк 11 назад отступают на величину 41,50 – 41,45 = 0,05 м и по перпендикуляру откладывают у = 1,72 м.
|

 1. Способ прямоугольных координат (в открытой местности при больших радиусах R).
1. Способ прямоугольных координат (в открытой местности при больших радиусах R). , по значению b вычисляются координаты точек 1, 2, 3 и т.д. по формулам:
, по значению b вычисляются координаты точек 1, 2, 3 и т.д. по формулам: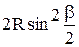 ;
; . (9.7)
. (9.7)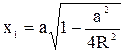 ;
; ;
;  . (9.8)
. (9.8)
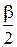 вычисляют по формуле sin
вычисляют по формуле sin  . (9.9)
. (9.9)
 9.4.3. Вынос пикета на кривую
9.4.3. Вынос пикета на кривую = 1100 – 1058,50 = 41,50 м.
= 1100 – 1058,50 = 41,50 м. вычисляют (9.10)
вычисляют (9.10) ,
,


