Модели решений функциональный и Вычислительных задач
5.1. Основные понятия В повседневной жизни, на производстве, в научно-исследовательской, инженерной или любой другой деятельности человек постоянно сталкивается с решением задач. Задачи, которые мы решаем, по своему назначению можно разделить на две категории:. вычислительные задачи целью которых является определение неко-торой величины, и функциональные задачи, предназначенные для создания некого аппарата, выполняющего определенные действия — функции. Например, проектирование нового здания требует реше-нияя задачи расчета прочности его фундамента, несущих опорных конструкций, расчета финансовых затрат на строительство, определение оптимального числа работников и т.д. Для повышения производительности труда строителей создано немало машин функционального назначения (решены функциональные задачи), такие как экскаватор, бульдозер, подъемный кран и др. История развития средств вычислительной техники повествует о том, что мощным толчком для создания первых вычислительных машин стала вторая мировая война. Для успешного ведения войны требовалось решать множество вычислительных задач. Немецкий инженер Конрад Цузе сконструирован вычислительную машину Z2 (1941 г.) для выполнения необходимых расчетов при проектировании самолетов и баллистических снарядов. Английские инженеры создали вычислительную машину «Колосс» (1943 г.) для дешифровки перехваченных сообщений вражеской армии. Американский инженер Говард Эйкен для выполнения баллистических расчетов создал компьютер «Марк I» (1944 г.). Компьютеры первого и второго поколения использовались для решения вычислительных задач, для инженерных, научных, финансовых расчетов, для обработки больших объемов данных. Начиная с третьего поколения, область применения ЭВМ включает и решение функциональных задач: это обработка баз данных, управление, проектирование. Современный компьютер может выполнять практически любые задачи, а массовое использование персональных компьютеров и повсеместное применение новых информационных технологий отводит ему особую роль для решения любых задач. С точки зрения информатики, решение любой задачи представляет замкнутую технологическую последовательность (рис. 5.1):
Рис. 5.1. Этапы решения задачи В этом ряду каждый элемент играет свою особую роль. Объектом (от лат. objectum — предмет) называется все то, что противостоит субъекту в его практической и познавательной деятельности, все то, на что направлена эта деятельность. Под объектами понимаются предметы и явления, как доступные, так и недоступные чувственному восприятию человека, но имеющие видимое влияние на другие объекты (например, гравитация, инфразвук _или электро-магнитные волны). Объективная дальность, существующая независимо от нас, является объектом для человека в любой его деятельности и взаимодействует с ним. Поэтому объект всегда должен рассматриваться во взаимодействии с другими объектами, с учетом их взаимовлияния. Деятельность.человека обычно идет по д вум направлениям:Ис -следование _ свойств объекта с целью их использования (или нейтра-лизации) создание новых обьектов,имеющих полезныесвойства. Первое направление относится к научным исследованиям и большую роль при их проведении имеет г ипотеза, т.е. предсказание свойств объекта при недостаточной его изученности. Второе направление относится к инженерному проектированию. При этом важную роль играет понятие аналогии- суждение о каком-либо сходстве известного и проектируемого объекта. Аналогия может быть полной или частичной. Это понятие относительно и определяется уровнем абстрагирования и целью построения аналогии. Любой аналог (образ) _ какого-либо объекта, процесса или явления. используемый в качестве заменителя (представителя) оригинала, называется моделью (от лат, modulus - образец).
Если результаты моделирования подтверждаются и могут служить основой для прогнозирования поведения исследуемых объектов, то говорят, что модель адекватна объекту. Степень адекватности зависит от цели и критериев моделирования.
Имитационное моделирование предполагает построение модели с характеристиками, адекватными оригиналу на основе какого-либо его физического или информационного принципа. Это означает, что внешнее воздействие на модель объект вызывают идентичные изменения свойств оригинала и модели. При таком моделировании отсутствует общая аналитическая модель большой размерности а объект представлен системой, состоящей из элементов, взаимодействующих между собой и с внешним миром. Задавая внешние воздействия, можно получить характеристики системы и провести их анализ...В последнее время имитационное моделирование все больше ассоциируется с моделированием: объектов на Компьютере, что позволяет в интерактивном режиме исследовать модели самых разных по природе объектов.
5.2. Системный подход в моделировании систем Классический (или индуктивный ) подход к моделированию рассматривает систему, переходя от часного к общему, и синтезирует ее путем слияния компонент, разрабатываемых отдельно. Системный подход предполагает последовательный переход от общего к часному,. когда в основе рассмотрения лежит цель, при этом объект выде-ляется из окружающего мира. ' При создании нового объекта с полезными свойствами (например, системы управления) задаются критерии, определяющие степень полезности полученных свойств. Так как любой объект моделирования представляет собой систему взаимосвязанных элементов, введем понятие системы. Система S есть целенаправленное множество взаимосвязанных элементов любой природы. Внешняя среда Е представляет собой множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздействием. При системном подходе к моделированию прежде всего четко определяется цель моделирования. Создание модели полного аналога оригинала дело трудоемкое и дорогое, поэтому модель создается под определенную цель. Важным для системного подхода является определение структуры системы совокупности связей между элеметами системы отражающих их взаимодействие. Существует ряд походов к исследованию систем и ее свойств, к которым следует отнести структурный и функциональный. При структурном подходе выявляется состав выделенных элементов системы S и связи между ними. Совокупность элементов и связей позволяет судить о свойствах выделенной части системы. При функциональном подходе рассматриваются функции (алгоритмы поведения системы, причем, каждая функция описывает поведение одного свойства при внешнем воздействии Е. Такой подход не требует знания структуры системы, а ее описание состоит из набора функций ее реакции на внешние воздействия. Классический метод построения модели использует функциональный подход, при котором в качестве элемента модели принимается компонента, описывающая поведение одного свойства и не отображающая реальный состав элементов. Кроме этого компоненты системы являются изолированными друг от друга, что плохо отражает моделируемую систему. Такой метод построения модели приме -ним лишь для простых систем, так как требует включения в состав функций, описывающих свойства системы, отношения между свойствами, которые могут быть плохо определены или неизвестны. С усложнением моделируемых систем, когда невозможно учесть все взаимовлияния свойств, применяется системный метод, основанный на структурном подходе. При этом система S разбивается на ряд подсистем Ss со своими свойствами, которые, естественно, проще описать функциональными зависимостями, и определяются связи между подсистемами. В этом случае система функционирует в соответствии со свойствами отдельных подсистем и связей между ними. Это избавляет от необходимости описывать функционально взаимосвязи между свойствами системы 5, делает модель более гибкой, так как изменение свойств одной из подсистем автоматически изменяет свойства системы. 5.3. Классификация видов моделирования В зависимости от характера изучаемых процессов в системе S и цели моделирования существует множество типов моделей и способов их классификации, например по цели использования наличию случайных воздейвий, отношению ко времени, возможности реализации, облости применения и др. (таблица) По цели использования модели классифицируются на научный эк сперимент, в котором осуществляется исследование модели с применением различных средств получения данных об объекте, возможности влияния на ход процесса, с целью получения новых данных об объекте или явлении; комплексные испытания и производственный эксперимент, использующие натурное испытание физического объекта для получения высокой достоверности о его характеристиках; оп- тимизационные, связанные с нахождением оптимальных показателей системы (например, нахождение минимальных затрат или определение максимальной прибыли). По наличию воздействий на систему модели делятся не детерминированные (в системах отсутствуют случайные воздействия) и с moхастические (в системах присутствуют вероятностные воздействия). Эти же модели некоторые авторы классифицируют по способу оценки Классификации видов моделей
параметров системы: в детерминированных системах параметры модели оцениваются одним показателем для конкретных значений их исходных данных; в стохастических системах наличие вероятностных характеристик исходных данных позволяет оценивать параметры системы несколькими показателями. .По отношению ко времени модели разделяют на статические, описывающие систему в определенный момент времени, и динамические, рассматривающие поведение системы во времени. В свою очередь, динамические модели подразделяют на дискретные, в которых все события происходят по интервалам времени, и непрерывные, где все события происходят непрерывно во времени. По возможности реализации модели классифицируются как мыс ленные, описывающие систему, которую трудно или невозможно моделировать реально, реальные, в которых модель системы представлена либо реальным объектом, либо его частью, и» информационные, реализующие информационные процессы (возникновение, передачу, обработку и использование информации) на компьютере. В свою очередь, мысленные модели разделяют на наглядные(при которых моделируемые процессы и явления протекают наглядно) символические (модель системы представляет логический объект, в котором основные свойства и отношения реального объекта выражены системой знаков или символов) и математические (представляют системы математических объектов, позволяющие получать исследуемые характеристики реального объекта). Реальные модели делят на натурные (проведение исследования на реальном объекте и последующая обработка результатов эксперимента с применением теории подобия) и физические (проведение исследования на установках, которые сохраняют природу явления и обладают физическим подобием). По области применения модели подразделяют на универсальные, предназначенные для использования многими системами, и специализированные, созданные для исследования конкретной системы. 5.4, Математические модели Наиболее важным этапом при построении модели является переход от содержательного описания к формальному, что объясняется участием на этом этапе специалистов в предметной области, где существует моделируемая система, и специалистов в области моделирования систем. Наиболее удобным языком для их общения, целью которого является построение адекватной модели системы, обычно, является язык математических описаний. Математическое описание системы компактно и удобно для дальнейших реализаций на компьютере, с целью проведения статистических испытаний, поэтому рассмотрим эти модели в первую очередь. 5.4,1. Построение математической модели системы Систему S можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих следующие подмножества: подмножество входных воздействий:
(или вектор входящих воздействий х = {х],х2)...>хп }); подмножество воздействий внешней среды:
или вектор воздействия внешней среды подмножество собственных параметров системы:
(или вектор внутренних параметров подмножество выходных характеристик системы:
(или вектор выходных характеристик Подмножества X, V и H являются независимыми (экзогенными), Y является зависимым (эндогенным) подмножеством. Процесс функционирования системы описывается во времени оператором F, который преобразует экзогенные переменные в эндогенные в соответствии с соотношением Эта зависимость называется называется выходной траекторией y(t). Соотношение (*) является математическим описанием поведением системы во времени, поэтому модели такого типа называются динамическими моделями. Если закон функционирования у не содержит параметра времени, то такие модели называются статическими и отображают связь между подмножеством у и подмножествамии записывается
Если в динамической модели дискретизировать время, то в каждый момент времени можно определить состояние системы
Первое уравнение по начальному состоянию z° и экзогенным переменным определяет следующее состояние, а второе по значению состояния z определяет эндогенные переменные на выходе системы. 5.4.2. Примеры построения динамических моделей При моделировании непрерывных динамических объектов в качестве моделей обычно выступают дифференциальные уравнения, связывающее поведение объекта со временем. Положительным свойством дифференциальных уравнений является то, что одно и то же уравнение моделирует системы различной физической природы. В качестве независимой переменной в динамических системах обычно выступает время, от которого зависят неизвестные значения искомой функции, определяющие поведения объекта. Математическое описание модели в общем виде:
— n-мерные векторы и непрерывна
Например, процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением
Процесс в электрическом колебательном контуре
Очевидно, что если положить
описывающее состояние во времени обеих систем
Общая математическая модель позволяет исследовать одну систему, моделируя работу другой. Рассмотрим пример построения дифференциальной модели объекта. Имеется сосуд, площадь горизонтального сечения которого является функцией расстояния сечения от дна сосуда. В начальный момент времени t = 0 высота уровня жидкости равна h метров. Площадь сечения сосуда на высоте х равна S(x), В дне сосуда имеется отверстие площадью s. Определить зависимость уровня воды в сосуде от времени x(t). Из физики известно, что скорость истечения жидкости v в тот момент, когда высота ее уровня равна х, определяется равенством
Полученное дифференциальное уравнение дает зависимость уровня воды в сосуде от времени x(t). Решим теперь конкретную задачу, выбрав сосуд с известным S(x). Пусть имеется цилиндрический сосуд радиусом R с круглым отверстием в дне радиусом г, наполненный водой. Площадь поперечного сечения сосуда постоянна и не зависит от
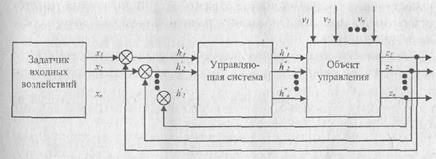
Это уравнение может быть решено аналитически или одним из численных методов. Модели динамических систем на основе дифференциальных уравнений нашли широкое применение в теории управления различными техническими объектами. Под влиянием неизвестных заранее возмущений фактическое поведение системы отклоняется от желаемого, задаваемого алгоритмом и для приближения ее поведения к необходимому значению, в состав системы вводится автоматическое управление системой. Оно может быть встроено в саму систему, но при моделировании блок управления отделяется от самой системы. В общем виде структура многомерной системы автоматического управления (САУ) представлена на рис. 5.2.
Рис. 5.2. Структура многомерной системы автоматического управления Эндогенные переменные: управляющих воздействий, соответственно. Экзогенные переменные: z(t) — вектор состояния системы, который обычно совпадает с век- тором выходных переменных, т.е. делировании САУ см.: «Теория автоматического управления»: Учебник для машиностроит. спец. вузов/ Под ред. Ю.М. Соломенцева. М.: Высшая школа, 1999.) 5.5. информационные модели 5,5.1, информационные объекты и связи Информационные модели во многих случаях опираются на математические модели, так как при решении задач математическая модель исследуемого объекта, процесса или явления неизбежно преобразуется в информационную для ее реализации на компьютере. Определим основные понятия информационной модели. Информационным объектом называется описание реального объекта, процесса или явления в виде совокупности его характеристик (информационных элементов), называемых реквизитами. Информационный объект определенной структуры (реквизитного состава) образует тип (класс), которому присваивают уникальное имя. Информационный объект с конкретными характеристиками называют экземпляром. Каждый экземпляр идентифицируется заданием ключевого реквизита (ключа). Одни и те же реквизиты в различных информационных объектах могут быть как ключевыми, так и описательными. Информационный объект может иметь несколько ключей. Пример. Информационный объект СТУДЕНТ имеет реквизитный Отношения, существующие между реальными объектами, определяются в информационных моделях как связи. Существует три вида связей: один к одному Связь один к одному определяет соответствие одному экземпляру информационного объекта X не более одного экземпляра информационного объекта Y, и наоборот. Пример. Информационные объекты СТУДЕНТ и ЛИЧНОЕ ДЕЛО будут связаны отношением один к одному. Каждый студент имеет определенные уникальные данные в личном деле.
При связи один ко многим одному экземпляру информационного объекта X может соответствовать любое количество экземпляров информационного объекта Y, но каждый экземпляр объекта Y связан не более чем с одним экземпляром объекта X. Пример. Между информационными объектами МЕСТО ОБУЧЕНИЯ и СТУДЕНТ необходимо установить связь один ко многим. Одно и то же место обучения может многократно повторяться для различных студентов. Связь многие ко многим предполагает соответствие одному экземпляру информационного объекта X любое количество экземпляров объекта Y, и наоборот. Пример. Информационные объекты СТУДЕНТ и ПРЕПОДАВАТЕЛЬ имеют связь многие ко многим. Каждый студент обучается у множества преподавателей, а каждый преподаватель учит множество студентов. 5.5.2. Примеры информационных моделей Определим информационную модель как связанную совокупность информационных объектов, описывающих информационные процессы в исследуемой предметной области. Существующие информационные модели разделим на универсальные и специализированные. Универсальные модели предназначены для использования в различных предметных областях, к ним относятся: базы данных и системы управления базами данных, автоматизированные системы управления, базы знаний, экспертные системы. Специализированные модели предназначены для описания конкретных систем, являются уникальными по своим возможностям, более дорогостоящими. Рассмотрим некоторые универсальные модели.
Базы данных представляют связанную совокупность структурированных данных, относящихся к определенному процессу или явлению, в конкретной предметной области. Система управления базами данных представляет собой программный комплекс для создания, организации необходимой обработки, хранения и передачи баз данных. Ядром любой БД является модель представления данных. Модель данных представляет множество структур данных и взаимосвязи между ними. Различают иерархическую, сетевую и реляционную модели данных. Иерархическая модель представляет связи между объектами (данными) в виде дерева. К основным понятиям иерархической модели относятся: • узел — набор атрибутов данных, описывающих объект; • связь - линия, связывающая узлы нижнего уровня с одним уз • уровень - номер слоя узлов, отсчитанный от корня. Рис. 5.3. Иерархическая модель данных
Количество деревьев в БД определяется числом корневых записей. К каждому узлу существует единственный путь от корня. Сетевая структура имеет те же составляющие, что и иерархическая, но каждый узел может быть связан с любым другим узлом (рис. 5.4). Сетевой подход к организации данных является расширением иерархического. В иерархических моделях запись-потомок должна иметь только одного предка; в сетевых — потомок может иметь любое число предков.
Рис. 5.4. Сетевая модель данных Обе эти модели не получили широкого распространения из-за сложности реализации графов в виде машинных структур данных, кроме того, в них сложно осуществить операции поиска информации. Набольшее распространение получила третья модель данных - реляционная, она может так же описывать иерархическую и сетевую модель. Реляционная модель ориентирована на организацию данных в виде двумерных таблиц и подробно рассмотрена в 4.4.3. искусственный интеллект Идеи моделирования человеческого разума известны с древнейших времен. Впервые об этом упоминается в сочинении философа и теолога Раймунда Луллия (ок.1235 - ок.1315) «Великое искусство», который не только высказал идею логической машины для решения разнообразных задач, исходя из всеобщей классификации понятий (XIV в.), но и попытался ее реализовать. Рене Декарт (1596—1650) и Готфрид Вильгельм Лейбниц (1646-1716) независимо друг от друга развивали учение о прирожденной способности ума к познанию и всеобщих и необходимых истин логики и математики, работали над созданием универсального языка классификации всех знаний. Именно на этих идеях базируются теоретические основы создания искусственного интеллекта. Толчком к дальнейшему развитию модели человеческого мышления стало появление в 40-х гг. XX в. ЭВМ. В 1948 г. американский ученый Норберт Винер (1894-1964) сформулировал основные положения новой науки - кибернетики. В 1956 г. в Стенфордском университете (США) на семинаре под названием «Artificial intelligence» (искусственный интеллект), посвященном решению логических задач, признано новое научное направление, связанное с машинным моделированием человеческих интеллектуальных функций и названное искусственный интеллект. Вскоре эта отрасль разделилась на два основных направления: нейрокибернетику и кибернетику «черного ящика». Нейрокибернетика обратилась к структуре человеческого мозга как единственно мыслящему объекту и занялась его аппаратным моделированием. Физиологи давно выявили нейроны — связанные друг с другом нервные клетки как основу мозга. Нейрокибернетика занимается созданием элементов, аналогичных нейронам, и их объединением в функционирующие системы, эти системы называют нейросетями. В середине 80-х гг. XX в. в Японии был создан первый нейрокомпьютер, моделирующий структуру человеческого мозга. Его основная область применения — распознавание образов. Кибернетика «черного ящика» использует другие принципы, структура модели не главное, важна ее реакция на заданные входные данные, на выходе модель должна реагировать как человеческий мозг. Ученые этого направления занимаются разработкой алгоритмов решения интеллектуальных задач для имеющихся вычислительных систем. Наиболее значимые результаты: • Модель лабиринтного поиска (конец 50-х гг.), в которой рассматривается граф состояний объекта и в нем происходит поиск оптимального пути от входных данных к результирующим. На • Эвристическое программирование (начало 60-х гг.) разрабатывало • Методы математической логики. Метод резолюций, позволяющий на основе определенных аксиом автоматически доказывать
С середины 70-х гг. реализуется идея моделирования конкретных знаний специалистов-экспертов. В США появляются первые экспертные системы. Возникает новая технология искусственного интеллекта, основанная на представлении и использовании знаний. С середины 80-х гг. искусственный интеллект коммерциализируется. Растут капиталовложения в эту отрасль, появляются промышленные экспертные.системы, повышается интерес к самообучающимся системам.
При изучении интеллектуальных систем необходимо выяснить, что представляют собой знания и в чем их отличие от данных. Понятие знания определяют по-разному, но какого-либо исчерпывающего определения нет. Приведем некоторые из определений: Знания — выявленные закономерности предметной области (принципы, связи, законы), позволяющие решать задачи в этой области. Знания — хорошо структурированные данные, или данные о данных, или метаданные. Знания - совокупность сведений, образующих целостное описание, соответствующее некоторому уровню осведомленности об описываемом вопросе, объекте и т.д. С точки зрения искусственного. интеллекта знания определяют как формализованую информацию, на которую ссылаются.в.процессе, логического вывода. Для хранения знаний используют базы знаний. База. знаний -основа любой интеллектуальной системы. С точки зрения решения задач в некоторой предметной области Кроме того, знания делят на процедурные и декларативные .. Исторически первыми появились процедурные знания, «рассыпанные» в алгоритмах. Они управляли данными. Для их изменения требовалось вносить изменения в программы. С развитием искусственного ОБРАТНЫЙ ВЫВОД: Подтвердить выбранную цель с помощью имеющихся правил и данных-. 3-й проход: Шаг 1. Цель - «электронная коммерция»: Проверяем Пр. 1, данных «знакомство с Интернет» нет, они становятся новой целью, и есть правило, где она в правой части. Шаг 2. Цель — «знакомство с Интернет»: Пр. 2 подтверждает цель и активизирует ее. 2-й проход:. Шаг 3. Пр. 1 подтверждает искомую цель. Продукционная модель привлекает разработчиков наглядностью, модульностью, легкостью внесения дополнений и изменений, простотой механизма логического вывода, чаще всего используется в промышленных экспертных системах. Семантика - это наука, исследующая свойства знаков и знаковых систем, их смысловую связь с реальными объектами. Семантическая сеть - это ориентированный граф, вершины которого есть понятия, а дуги - отношения между ними (рис. 5.5). Это наиболее общая модель знаний, так как в ней имеются средства всех характерных для знаний свойств: внутренней интерпретации, структурированности, семантической метрики и активности.
Рис. 5.5. Семантическая сеть Достоинствами сетевых моделей являются: большие выразительные возможности; наглядность системы знаний, представленной графически; близость структуры сети, представляющей систему знаний, семантической структуре фраз на естественном языке; соответствие современным представлениям об организации долговременной памяти человека. К недостаткам отнесем то, что сетевая модель не содержит ясного представления о структуре предметной области, которая ей соответствует, поэтому ее формирование и модификация затруднительны; сетевые модели представляют собой пассивные структуры, для их обработки используется специальный аппарат формального вывода. Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети поставленной задачи, что, в свою очередь, говорит еще об одном недостатке модели — сложность поиска вывода на семантических сетях. Сетевые модели являются наглядным и достаточно универсальным средством представления знаний. Однако их формализация в конкретных моделях представления, использования и модификации знаний представляет достаточно тр
|




 Исследование объектов, процессов или явлений путем построения и изучения их моделей для определения или уточнения характеристик оригинала называется моделированием. Моделирование может
Исследование объектов, процессов или явлений путем построения и изучения их моделей для определения или уточнения характеристик оригинала называется моделированием. Моделирование может Все многообразие способов моделирования, рассматриваемого теорией моделирования, можно условно разделить на две группы: / аналитическое и имитационное моделирование. Аналитическое моделирование заключается в построении модели, основанной на описании поведения объекта или системы объектов в виде аналитических выражений — формул. При таком моделировании объект описывается системой линейных или нелинейных алгебраических или дифференциальных уравнений, решение которых может дать представление о свойствах объекта К полученной аналитической модели, с учетом вида и сложности формул применяются аналитические или приближенные численные методы., Реализация численных методов" обычно возлагается на вычислительные машины, обладающие большими вычислительными мощностями. Тем не менее, применение аналитического моделирования ограничено сложностью получения и анализа выражений для больших систем.
Все многообразие способов моделирования, рассматриваемого теорией моделирования, можно условно разделить на две группы: / аналитическое и имитационное моделирование. Аналитическое моделирование заключается в построении модели, основанной на описании поведения объекта или системы объектов в виде аналитических выражений — формул. При таком моделировании объект описывается системой линейных или нелинейных алгебраических или дифференциальных уравнений, решение которых может дать представление о свойствах объекта К полученной аналитической модели, с учетом вида и сложности формул применяются аналитические или приближенные численные методы., Реализация численных методов" обычно возлагается на вычислительные машины, обладающие большими вычислительными мощностями. Тем не менее, применение аналитического моделирования ограничено сложностью получения и анализа выражений для больших систем.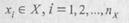
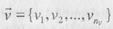 );
);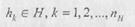
 );
);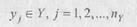
 ).
).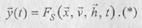 законом функционирования системы S. Закон функционирования F может быть задан в виде функции, функционала, логических условий, алгоритмически или таблично, а также в видесловесного набора правил соответствия. Совокупность зависимостей выходных характеристик системы от времени
законом функционирования системы S. Закон функционирования F может быть задан в виде функции, функционала, логических условий, алгоритмически или таблично, а также в видесловесного набора правил соответствия. Совокупность зависимостей выходных характеристик системы от времени
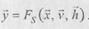 .
. . Множество Z всех возможных состояний системы называется пространством состояний системы. Процесс функционирования системы, изменяющей свое состояние в фиксированные моменты времени, можно описать векторными уравнениями
. Множество Z всех возможных состояний системы называется пространством состояний системы. Процесс функционирования системы, изменяющей свое состояние в фиксированные моменты времени, можно описать векторными уравнениями
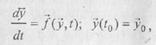





 где к ~ коэффициент скорости истечения жидкости из отверстия. На бесконечно малом промежутке времени dt истечение жидкости можно считать равномерным, а поэтому за время dt вытечет столбик жидкости, высота которого v dt и площадь сечения s, что, в свою очередь, вызовет понижение уровня жидкости в сосуде на - dx. Приравнивая объем жидкости, вытекшей из отверстия и из сосуда, получим
где к ~ коэффициент скорости истечения жидкости из отверстия. На бесконечно малом промежутке времени dt истечение жидкости можно считать равномерным, а поэтому за время dt вытечет столбик жидкости, высота которого v dt и площадь сечения s, что, в свою очередь, вызовет понижение уровня жидкости в сосуде на - dx. Приравнивая объем жидкости, вытекшей из отверстия и из сосуда, получим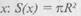 , площадь отверстия в дне
, площадь отверстия в дне 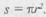 Для воды коэффициент к = 0,6. Подставив эта значения в уравнение, получим
Для воды коэффициент к = 0,6. Подставив эта значения в уравнение, получим
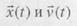 — вектора входных и возмущающих воздействий, а также
— вектора входных и возмущающих воздействий, а также  - вектора ошибок и
- вектора ошибок и . (Более подробно о мо-
. (Более подробно о мо-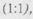 один ко многим
один ко многим 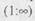 и многие ко многим
и многие ко многим 






