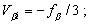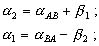Понятие о триангуляции

Триангуляция представляет собой группу примыкающих один к другому треугольников, в которых измеряют все три угла; два или более пунктов имеют известные координаты, координаты остальных пунктов подлежат определению. Группа треугольников образует либо сплошную сеть, либо цепочку треугольников.

Координаты пунктов триангуляции как правило вычисляют на ЭВМ по программам, реализующим алгоритмы строгого уравнивания по МНК. На стадии предварительной обработки триангуляции последовательно решают треугольники один за другим. В нашем курсе геодезии мы рассмотрим решение лишь одного треугольника.

В первом треугольнике ABP (рис.2.24) известны координаты двух вершин (A и B) и его решение выполняют в следующем порядке:

Рис.2.24. Единичный треугольник триангуляции

1. Вычисляют сумму измеренных углов ,
2. Принимая во внимание, что в треугольнике Σβ = 180^о, вычисляют угловую невязку:

1. Поскольку

то

Это уравнение содержит три неизвестных поправки β и решить его можно лишь при наличии двух дополнительных условий.

Эти условия имеют вид:

откуда следует, что

1. Вычисляют исправленные значения углов:

1. Решают обратную задачу между пунктами A и B вычисляют дирекционный угол α_AB и длину S₃ стороны AB.
2. По теореме синусов находят длины сторон AP и BP:

1. Вычисляют дирекционные углы сторон AP и BP:

1. Решают прямую геодезическую задачу из пункта A на пункт P и для контроля - из пункта B на пункт P; при этом оба решения должны совпасть.

В сплошных сетях триангуляции кроме углов в треугольниках измеряют длины отдельных сторон треугольников и дирекционные углы некоторых направлений; эти измерения выполняются с большей точностью и играют роль дополнительных исходных данных. При уравнивании сплошных сетей триангуляции в них могут возникнуть следующие условия:

• условия фигуры,
• условия суммы углов,
• условия горизонта,
• полюсные условия,
• базисные условия,
• условия дирекционных углов,
• координатные условия.

Формула для подсчета количества условий в произвольной сети триангуляции имеет вид:

где n - общее количество измеренных углов в треугольниках,
k - число пунктов в сети,
g - количество избыточных исходных данных.