Двосторонню критичну область знаходять виходячи з умови, що при справедливості нульової гіпотези сума ймовірностей того, що критерій прийме значення менше  або більше
або більше  , буде дорівнювати прийнятому рівню значущості
, буде дорівнювати прийнятому рівню значущості 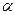
 .
.
Якщо критичні точки є симетричними, тоді


Розділ 15.3. Перевірка гіпотези про рівність дисперсій двох генеральних сукупностей
На практиці задача порівняння дисперсій виникає, якщо необхідно порівняти точність приладів, інструментів, методів вимірювань і т.п. Зрозуміло, що більш точним є пристрій, що забезпечує найменше розсіювання результатів вимірювань, тобто найменшу дисперсію.
 Нехай генеральні сукупності Х і У розподілені нормально. За незалежними вибірками обсягів
Нехай генеральні сукупності Х і У розподілені нормально. За незалежними вибірками обсягів  і
і  , що вилучені із цих генеральних сукупностей, знайдено виправлені вибіркові дисперсії
, що вилучені із цих генеральних сукупностей, знайдено виправлені вибіркові дисперсії  і
і  . Необхідно за виправленими дисперсіями, при заданому рівні значущості
. Необхідно за виправленими дисперсіями, при заданому рівні значущості 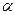 , перевірити нульову гіпотезу про рівність генеральних дисперсій розглянутих сукупностей
, перевірити нульову гіпотезу про рівність генеральних дисперсій розглянутих сукупностей
 . (15.1)
. (15.1)
За критерій перевірки нульової гіпотези (15.1) про рівність генеральних дисперсій, візьмемо відношення більшої виправленої дисперсії до меншої, тобто випадкову величину
 . (15.2)
. (15.2)
Випадкова величина 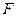 має розподіл Фішера-Снедекора із степенями свободи
має розподіл Фішера-Снедекора із степенями свободи  і
і  , де
, де  - обсяг вибірки, за якою обчислена більша виправлена дисперсія,
- обсяг вибірки, за якою обчислена більша виправлена дисперсія,  - обсяг вибірки, за якою обчислена менша виправлена дисперсія.
- обсяг вибірки, за якою обчислена менша виправлена дисперсія.
 Методика перевірки нульової гіпотези
Методика перевірки нульової гіпотези  при конкуруючий гіпотезі
при конкуруючий гіпотезі 
Для того, щоб при заданому рівні значущості, перевірити нульову гіпотезу  про рівність генеральних дисперсій нормальних сукупностей, при конкуруючий гіпотезі
про рівність генеральних дисперсій нормальних сукупностей, при конкуруючий гіпотезі  , необхідно обчислити спостережувальне значення критерія
, необхідно обчислити спостережувальне значення критерія  і за таблицями критичних точок розподілу Фішера-Снедекора, за заданим рівнем значущості
і за таблицями критичних точок розподілу Фішера-Снедекора, за заданим рівнем значущості 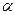 і числом степеней свободи
і числом степеней свободи  і
і  ,
,  - число степеней свободи більшої дисперсії, знайти критичну точку
- число степеней свободи більшої дисперсії, знайти критичну точку  . Якщо
. Якщо  , тоді немає підстав відкидати нульову гіпотезу. Якщо
, тоді немає підстав відкидати нульову гіпотезу. Якщо  , тоді нульову гіпотезу відкидаємо.
, тоді нульову гіпотезу відкидаємо.
 Приклад:
Приклад:
За двома незалежними вибірками обсягів  і
і 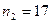 , вилучених із нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії
, вилучених із нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії  і
і  . При рівні значущості
. При рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу  при конкуруючий гіпотезі
при конкуруючий гіпотезі  .
.
Рішення
Обчислимо спостережувальне значення критерія
 .
.
За таблицею критичних точок Фішера-Снедекора за заданим рівнем значущості  і числом степеней свободи
і числом степеней свободи  і
і  , знайдемо критичну точку
, знайдемо критичну точку
 .
.
Якщо 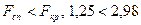 , тоді немає підстав відкидати нульову гіпотезу.
, тоді немає підстав відкидати нульову гіпотезу.
 Методика перевірки нульової гіпотези
Методика перевірки нульової гіпотези  при конкуруючий гіпотезі
при конкуруючий гіпотезі 
Для того, щоб при заданому рівні значущості, перевірити нульову гіпотезу  про рівність генеральних дисперсій нормальних сукупностей, при конкуруючій гіпотезі
про рівність генеральних дисперсій нормальних сукупностей, при конкуруючій гіпотезі  , необхідно обчислити спостережувальне значення критерія
, необхідно обчислити спостережувальне значення критерія  і за таблицями критичних точок розподілу Фішера-Снедекора, за заданим рівнем значущості
і за таблицями критичних точок розподілу Фішера-Снедекора, за заданим рівнем значущості  і числом степеней свободи
і числом степеней свободи  і
і  ,
,  - число степеней свободи більшої дисперсії, знайти критичну точку
- число степеней свободи більшої дисперсії, знайти критичну точку  . Якщо
. Якщо  , тоді немає підстав відкидати нульову гіпотезу. Якщо
, тоді немає підстав відкидати нульову гіпотезу. Якщо  , тоді нульову гіпотезу відкидаємо.
, тоді нульову гіпотезу відкидаємо.
 Приклад:
Приклад:
За двома незалежними вибірками обсягів  і
і 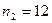 , вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії
, вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії  і
і 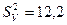 . При рівні значущості
. При рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу  при конкуруючій гіпотезі
при конкуруючій гіпотезі  .
.
Рішення
Обчислимо спостережувальне значення критерія
 .
.
За таблицею критичних точок Фішера-Снедекора за заданим рівнем значущості  і числом степеней свободи
і числом степеней свободи  і
і  , знайдемо критичну точку
, знайдемо критичну точку
 .
.
Якщо  , тоді немає підстав відкидати нульову гіпотезу.
, тоді немає підстав відкидати нульову гіпотезу.

 або більше
або більше  , буде дорівнювати прийнятому рівню значущості
, буде дорівнювати прийнятому рівню значущості 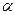
 .
.

 Нехай генеральні сукупності Х і У розподілені нормально. За незалежними вибірками обсягів
Нехай генеральні сукупності Х і У розподілені нормально. За незалежними вибірками обсягів  і
і  , що вилучені із цих генеральних сукупностей, знайдено виправлені вибіркові дисперсії
, що вилучені із цих генеральних сукупностей, знайдено виправлені вибіркові дисперсії  і
і  . Необхідно за виправленими дисперсіями, при заданому рівні значущості
. Необхідно за виправленими дисперсіями, при заданому рівні значущості  . (15.1)
. (15.1) . (15.2)
. (15.2)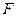 має розподіл Фішера-Снедекора із степенями свободи
має розподіл Фішера-Снедекора із степенями свободи  і
і  , де
, де  - обсяг вибірки, за якою обчислена менша виправлена дисперсія.
- обсяг вибірки, за якою обчислена менша виправлена дисперсія.
 і за таблицями критичних точок розподілу Фішера-Снедекора, за заданим рівнем значущості
і за таблицями критичних точок розподілу Фішера-Снедекора, за заданим рівнем значущості  - число степеней свободи більшої дисперсії, знайти критичну точку
- число степеней свободи більшої дисперсії, знайти критичну точку  . Якщо
. Якщо  , тоді немає підстав відкидати нульову гіпотезу. Якщо
, тоді немає підстав відкидати нульову гіпотезу. Якщо  , тоді нульову гіпотезу відкидаємо.
, тоді нульову гіпотезу відкидаємо. Приклад:
Приклад: і
і 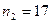 , вилучених із нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії
, вилучених із нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії  і
і  . При рівні значущості
. При рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу  .
. і
і  , знайдемо критичну точку
, знайдемо критичну точку .
.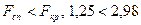 , тоді немає підстав відкидати нульову гіпотезу.
, тоді немає підстав відкидати нульову гіпотезу.
 і числом степеней свободи
і числом степеней свободи  . Якщо
. Якщо  і
і 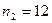 , вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії
, вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії  і
і 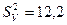 . При рівні значущості
. При рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу  .
. і числом степеней свободи
і числом степеней свободи  і
і  , знайдемо критичну точку
, знайдемо критичну точку .
. , тоді немає підстав відкидати нульову гіпотезу.
, тоді немає підстав відкидати нульову гіпотезу.


