Методика обчислення теоретичних частот нормального розподілу
1. Весь інтервал спостережувальних значень Х вибірки обсягу
2. Обчислюємо вибіркову середню 3. Нормуємо випадкову величину Х, тобто переходимо до величини
При цьому найменше значення 4. Обчислюємо теоретичні ймовірності
де 5. Обчислюємо шукані теоретичні частоти за формулою
Обчислити теоретичні частоти за заданим інтервальним розподілом вибірки обсягу
Рішення Результати розрахунків занесемо до таблиц 1 Таблиця 1
Знайдемо середню вибіркову: Знайдемо вибіркове середнє квадратичне відхилення:
Нормуємо випадкову величину Х за формулами (15.7), результати обчислень запишемо у 8 і 9 стовпці таблиці 2. Таблиця 2
За таблицею функції Лапласа знаходимо значення Обчислюємо теоретичні ймовірності Обчислюємо шукані теоретичні частоти за формулою (15.9) (стовпчик 5 продовження таблиці): Як бачимо,
Розділ 15.5. Завдання до заняття 15
1. Дати означення статистичної гіпотези. 2. Дати означення нульової і конкуруючої гіпотези. 3. Дати означення статистичного критерія. 4. Дати означення критичної області і області прийняття нульової гіпотези. 5. Дати означення і пояснити алгоритм побудови правосторонньої критичної області. 6. Дати означення і пояснити алгоритм побудови лівосторонньої критичної області. 7. Дати означення і пояснити алгоритм побудови двосторонньої критичної області. 8. Сформулювати правило перевірки нульової гіпотези 9. Сформулювати правило перевірки нульової гіпотези 10. Дати означення статистичного критерія згоди. 11. Сформулювати правило перевірки нульової гіпотези 12. Сформулювати методику обчислення теоретичних частот.
Розділ 1.6. Поняття кореляції При вивченні вищої математики користуються встановленими законами, однозначними залежностями одних величин від інших. Якщо кожному значенню змінної х за певним правилом або законом ставиться у відповідність одне певне значення змінної у, тоді говорять, що у є функцією від аргументу х і це записують як Але такі функціональні зв’язки мають обмежене розповсюдження. Особливо це стосується економічних, біологічних, суспільних явищ. Зміна даних явищ характеризується тим, що числовому значенню однієї ознаки відповідає не одна і та ж певна величина, а певна сукупність значень іншої, пов’язаної з нею ознаки. Так, чистий прибуток підприємства залежить не тільки від витрат на виробництво продукції і ціни на неї, але і від обсягів виробництва, можливості збуту виробленої продукції, її якісних показників тощо. Тому розглянутий зв’язок не може бути функціональним. Якщо числовому значенню деякого фактора х відповідає не конкретна величина, а групова середня результативного показника у, то таку залежність називають кореляційною. Кореляційний зв’язок є не точна, а ймовірносна залежність однієї ознаки від іншої. Цей зв’язок має різну степінь точності, від повної незалежності до функціональної залежності. Розділ 16.2. Метод найменших квадратів (загальні поняття) Означення: Статистичною називається залежність, при якій зміна однієї з величин веде до зміни розподілу іншої. Якщо зміна однієї з величин веде до зміни середнього значення іншої, тоді статистична залежність називається кореляційною. При вивченні закономірностей в деяких дослідженнях інженерної справи, економіки, біології, медицини і т.п. приходиться аналітично описувати (у вигляді формули) зв'язок між двома змінними x та y. Для цього в процесі експериментів та спостережень вимірюють з можливою точністю окремі значення xi і відповідні їм значення yi (i=1,2,…,n), або отримують такі значення як статистичні дані. В результаті маємо таблицю значень.
Побудуємо у вибраній системі координат XOY точки Mi(xi, yi), координати яких відповідають даним таблиці. Тепер виникає необхідність вибору відповідної функції y=f(x), яка б описувала зв'язок між x і y. Таку функцію називають емпіричною. В загальному випадку вибір емпіричної функції не є однозначним. Можна знайти лінію, яка б проходила через кожну з точок Mi, це може бути так званий інтерполяційний багаточлен (на рис. 1 це пунктирна лінія), порядок якого буде досить високим (на одиницю меншим, ніж кількість точок в таблиці). Крім того, дані таблиці можуть бути не досить точними внаслідок наявності похибок вимірювання, а також впливу інших факторів, які ми не завжди можемо врахувати. Тому дослідники віддають перевагу більш простим і зручнішим функціям, таким, як лінійна Позначимо через
де
Параметри функції
Розділ 16.3. Побудова рівняння лінійної функції
є функцією двох змінних a i b (xi, yi – числа з таблиці). За необхідною умовою існування екстремуму, функція S (a,b) приймає мінімальне значення при тих значеннях a i b, при яких частинні похідні по цих змінних дорівнюють нулю, тобто коли
Із формули (16.2) знаходимо
Прирівнюючи до нуля частинні похідні, отримуємо систему рівнянь
Система (16.3) називається нормальною системою методу найменших квадратів. Розв'язуючи систему рівнянь (16.3), знаходять числа a i b, які підставляють у рівняння Метод найменших квадратів був запропонований німецьким математиком К. Гауссом.
Статистичні дані чистого прибутку П підприємства і обсягів виробленої продукції
Припускаючи, що між змінними
Рішення
Складемо розрахункову таблицю.
За формулою (16.3) знайдемо коефіцієнти рівняння прямої лінії регресії
За формулами Крамера знайдемо розв’язок системи
Таким чином, рівняння прямої лінії регресії набуде вигляду
За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 2 представлено кореляційне поле, побудоване за статистичними даними, та рівняння прямої, побудоване за допомогою знайденого рівняння прямої лінії регресії.
Рис.2 Розділ 16.4. Побудова рівняння квадратичної функції
Знаходимо частинні похідні функції
Прирівнюючи кожну з похідних до нуля отримуємо систему лінійних відносно a, b, c рівнянь
Статистичні дані витрат В підприємства і вкладень у модернізацію обладнання М наведено у вигляді таблиці.
Припускаючи, що між змінними В i М існує квадратична залежність, знайти емпіричну формулу
Рішення Для спрощення обчислень позначимо витрати В через змінну у, а вкладення в модернізацію М через змінну х та складемо розрахункову таблицю.
Використовуючи формулу (16.4) складемо систему для знаходження коефіцієнтів
Знайдемо розв’язок системи рівнянь за формулами Крамера
Тоді шукане рівняння набуде вигляду
За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 3 представлено кореляційне поле, побудоване за статистичними даними, та рівняння параболи, побудоване за допомогою знайденого рівняння квадратичної лінії регресії.
Рис. 3
Розділ 16.5. Побудова рівняння гіперболічної функції
Після цього знаходиться мінімум функції
Для отримання системи (16.5) складається відповідна обчислювальна таблиця відносно значень
Статистичні дані собівартості продукції С підприємства і обсягів виробництва продукції Q наведено у вигляді таблиці.
Припускаючи, що між змінними C i Q існує гіперболічна залежність, знайти емпіричну формулу
Рішення
Для спрощення обчислень, позначимо собівартість виробленої продукції С через змінну у, а обсяги виробленої продукції Q через змінну х. Зробимо заміну
Для знаходження параметрів рівняння гіперболи, складемо систему (16.5), яку розв’яжемо за формулами Крамера
Тоді шукане рівняння набуде вигляду
За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 4 представлено кореляційне поле, побудоване за статистичними даними, та рівняння гіперболи, побудоване за допомогою знайденого рівняння вибіркової лінії регресії.
Рис.4 Розділ 16.6. Побудова рівняння показникової функції
Статистичні дані витрат на зберігання продукції, що потребує охолодження В і температури зберігання Т наведено у вигляді таблиці.
Припускаючи, що між змінними В i Т існує показникова залежність, знайти емпіричну формулу Рішення
Для спрощення обчислень позначимо витрати на зберігання продукції В через змінну у, а температуру зберігання Т через змінну х. Зробимо заміну
Аналогічно до методики побудови рівняння прямої, знайдемо коефіцієнти
Повертаємося до заміни
Таким чином, шукане рівняння набуде вигляду
За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 5 представлено кореляційне поле, побудоване за статистичними даними, та рівняння показникової функції, побудоване за допомогою знайденого рівняння вибіркової лінії регресії.
Рис. 5. Розділ 16.7.Знаходження параметрів множинної лінійної залежності
Досить поширене використання цієї залежності пояснюється відносною простотою як її побудови, так і інтерпритації параметрів. Застосуємо до обчислення параметрів залежності (16.6) метод найменших квадратів.
Одержуємо систему
Після елементарних перетворень одержуємо систему рівнянь, з якоъ знаходимо параметри рывняння (10.6).
(16.7)
Аналогічним чином, можна побудувати трьохфакторне рівняння
Після перетворень система (16.7) для визначення параметрів рівняння (16.8) набуде вигляду
Таблиця 1
Виробничі фонди, число працюючих і виробництво валової продукції підприємств
Підставимо значення сум у систему (16.9) і одержимо систему з чотирьох рівнянь і чотирьох невідомих.
Знайдемо розв’язок системи (наприклад за методом Гаусса)
Звідси, лінійна функція, що відображає зв’язок виробництва вадової продукції від суми основних і оборотних фондів та числа працюючих, набуде вигляду
Для перевірки точності обрахунків порівняємо емпіричні і теоретичні значення функції
Як видно, сумарні значення емпіричних і теоретичних частот співпадають.
Розділ 17.1. Кореляційна таблиця
Дата добавления: 2015-12-04; просмотров: 266. Нарушение авторских прав; Мы поможем в написании вашей работы! Психолого-педагогическая характеристика студенческой группы
Характеристика группы составляется по 407 группе очного отделения зооинженерного факультета, бакалавриата по направлению «Биология» РГАУ-МСХА имени К...
Этапы творческого процесса в изобразительной деятельности По мнению многих авторов, возникновение творческого начала в детской художественной практике носит такой же поэтапный характер, как и процесс творчества у мастеров искусства...
|

 Розглянемо один із способів обчислення теоретичних частот в припущенні, що генеральна сукупність розподілена нормально.
Розглянемо один із способів обчислення теоретичних частот в припущенні, що генеральна сукупність розподілена нормально. ділять на
ділять на  частинних інтервалів
частинних інтервалів  . Знаходять середини частинних інтервалів
. Знаходять середини частинних інтервалів  . Одержуємо варіаційний ряд
. Одержуємо варіаційний ряд






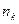
 і вибіркове середнє квадратичне відхилення
і вибіркове середнє квадратичне відхилення  .
. і обчислюємо кінці інтервалів
і обчислюємо кінці інтервалів  і
і  . (15.7)
. (15.7) , тобто
, тобто  , беруть рівним
, беруть рівним  , а найбільше
, а найбільше  беруть рівним
беруть рівним  .
.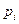 попадання Х в інтервал
попадання Х в інтервал  , (15.8)
, (15.8) - функція Лапласа.
- функція Лапласа. . (15.9)
. (15.9) Приклад:
Приклад: , припускаючи, що генеральна сукупність розподілена нормально.
, припускаючи, що генеральна сукупність розподілена нормально.
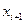









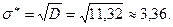




 і для значень
і для значень  ,
,  (стовпці 2 і 3 продовження таблиці).
(стовпці 2 і 3 продовження таблиці).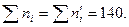
 Теоретичні питання до заняття 15
Теоретичні питання до заняття 15 про рівність генеральних дисперсій нормальних сукупностей при конкуруючій гіпотезі
про рівність генеральних дисперсій нормальних сукупностей при конкуруючій гіпотезі  .
. .
. : генеральна сукупність має нормальний розподіл.
: генеральна сукупність має нормальний розподіл. .
. Будь-які випадкові величини можуть бути пов’язані функціональною залежністю, що буває досить рідко, або залежністю іншого роду, яку називають статистичною, або будуть незалежними.
Будь-які випадкові величини можуть бути пов’язані функціональною залежністю, що буває досить рідко, або залежністю іншого роду, яку називають статистичною, або будуть незалежними. , квадратична
, квадратична  , показникові
, показникові 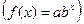 , гіперболічна
, гіперболічна  і ін. Обрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той або інший метод вибору емпіричної залежності
і ін. Обрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той або інший метод вибору емпіричної залежності  (на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри обраної залежності
(на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри обраної залежності 
 відхилення емпіричної функції в точці
відхилення емпіричної функції в точці 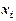 від відповідного табличного (експериментального) значення
від відповідного табличного (експериментального) значення  . Зрозуміло (див. рис. 1), що
. Зрозуміло (див. рис. 1), що  можуть бути для одних
можуть бути для одних  додатніми, а для інших від'ємними. Тому їх сума може навіть дорівнювати нулю. Краще було б брати суму їх абсолютних величин
додатніми, а для інших від'ємними. Тому їх сума може навіть дорівнювати нулю. Краще було б брати суму їх абсолютних величин  але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому
але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому , (16.1)
, (16.1) - теоретичне значення функції;
- теоретичне значення функції;  - статистичне значення функції.
- статистичне значення функції.
 обирають так, щоб сума квадратів S приймала найменше значення.
обирають так, щоб сума квадратів S приймала найменше значення. Розглянемо випадок, коли
Розглянемо випадок, коли  є лінійною функцією з невідомими параметрами a i b. Тоді величина відхилення
є лінійною функцією з невідомими параметрами a i b. Тоді величина відхилення  , а сума їх квадратів
, а сума їх квадратів . (16.2)
. (16.2)

 (16.3)
(16.3) що і дає формулу шуканої залежності.
що і дає формулу шуканої залежності. наведено у вигляді таблиці.
наведено у вигляді таблиці. за методом найменших квадратів.
за методом найменших квадратів.






 за формулою (16.1) знаходимо мінімум суми
за формулою (16.1) знаходимо мінімум суми  як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю
як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю

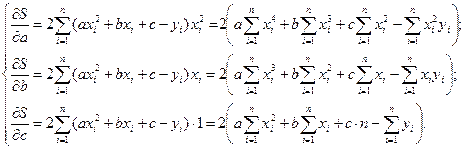
 (16.4)
(16.4) Приклад:
Приклад: за методом найменших квадратів.
за методом найменших квадратів.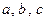








 здійснюється за допомогою заміни
здійснюється за допомогою заміни  В такому разі в таблицю значень потрібно доповнити значеннями
В такому разі в таблицю значень потрібно доповнити значеннями 












 яка має такий самий вид, як й лінійна функція, тому відповідна система запишеться
яка має такий самий вид, як й лінійна функція, тому відповідна система запишеться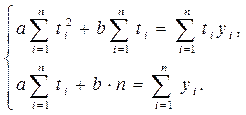 (16.5)
(16.5) з якої знаходять необхідні для системи суми. Після знаходження
з якої знаходять необхідні для системи суми. Після знаходження  отримуємо функцію
отримуємо функцію 
 за методом найменших квадратів.
за методом найменших квадратів. та складемо розрахункову таблицю.
та складемо розрахункову таблицю.






 Вирівнювання дослідних даних за показниковою функцією
Вирівнювання дослідних даних за показниковою функцією  здійснюється за допомогою логарифмування
здійснюється за допомогою логарифмування 
 і подальшою заміною
і подальшою заміною 
 Тоді отримаємо лінійну залежність
Тоді отримаємо лінійну залежність  параметри якої
параметри якої  знаходимо за розглянутим вище методом найменших квадратів.
знаходимо за розглянутим вище методом найменших квадратів. Приклад:
Приклад: за методом найменших квадратів.
за методом найменших квадратів. та складемо розрахункову таблицю.
та складемо розрахункову таблицю. і
і 











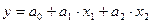 . (16.6)
. (16.6)


 . (16.8)
. (16.8) (16.9)
(16.9)











 .
.
 64,5
64,5

 При великій кількості спостережень одне й теж значення х може зустрічатися пх раз, одне й те ж значення у – пу раз, одна й таж пара чисел(х; у) може спостерігатися пху раз. Тому ці спостереження групуються, тобто підраховуються частоти пх, пу і пху. Всі згруповані дані записуються у вигляді таблиці, яку називають кореляційною.
При великій кількості спостережень одне й теж значення х може зустрічатися пх раз, одне й те ж значення у – пу раз, одна й таж пара чисел(х; у) може спостерігатися пху раз. Тому ці спостереження групуються, тобто підраховуються частоти пх, пу і пху. Всі згруповані дані записуються у вигляді таблиці, яку називають кореляційною.


