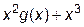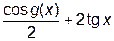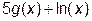Задача 1. 1.1 Постановка задачи и последовательность ее решения.
1.1 Постановка задачи и последовательность ее решения.
1.2 Формулы расчета коэффициентов аппроксимирующей кривой по методу наименьших квадратов, EXCEL –таблица и ее описание.
1.3 Аналитический вид полученной функции g (x) и совместный график «функция g (x) + экспериментальные точки».
1.4 Полная аналитическая запись и график функции F (g (x), x).
1.5 Формулы вычисления определенного интеграла методами средних прямоугольников и трапеций, уточнения по Ричардсону, EXCEL –таблица и ее описание.
1.6 Погрешности вычисленных значений и их анализ.
1.7 Вычисленное значение интеграла.
Задача 2
2.1 Постановка задачи и последовательность ее решения.
2.2 Формулы численного решения задачи Коши методами Эйлера и Рунге-Кутта, EXCEL -таблица и ее описание.
2.3 Графики полученных решений задачи Коши для обоих методов на одной диаграмме.
2.4 Исходные данные и формулы вычисления коэффициентов интерполяционного полинома Ньютона, EXCEL -таблица и ее описание.
2.5 Найденные коэффициенты полинома P 3(x), проверка выполнения условий Лагранжа и полная запись P 3(x).
2.6 Приведение уравнения P 3(x)=0 к виду, необходимому для использования метода простых итераций с условием его сходимости.
2.7 Формула вычислительного процесса метода простых итераций, критерий окончания процесса, EXCEL -таблица и ее описание.
2.8 Найденный корень уравнения.
Перечень использованной литературы.
ВАРИАНТЫ ЗАДАНИЙ
Таблица 1.1
Экспериментальные данные по зависимости g (x)
Подгруппа 1
| X
| З н а ч е н и я ф у н к ц и и g (x)
| | Вар.1
| Вар.2
| Вар.3
| Вар.4
| Вар.5
| Вар.6
| Вар.7
| Вар.8
| Вар.9
| | 2,00
| 6,842
| 15,330
| 1,408
| 21,315
| 1,878
| 3,319
| 1,544
| 11,009
| 3,274
| | 2,00
| 6,466
| 15,535
| 0,748
| 21,011
| 2,261
| 3,863
| 1,171
| 4,966
| 3,702
| | 2,00
| 6,816
| 15,592
| 1,153
| 21,491
| 2,452
| 3,956
| 0,911
| 4,610
| 4,220
| | 2,40
| 5,306
| 23,170
| 1,398
| 28,200
| 3,627
| 2,561
| 1,544
| 9,066
| 3,990
| | 2,80
| 5,557
| 33,668
| 1,766
| 39,554
| 5,384
| 1,436
| 0,588
| 10,458
| 5,896
| | 2,80
| 5,751
| 33,339
| 1,826
| 39,394
| 4,638
| 1,375
| 0,540
| 11,484
| 6,687
| | 3,20
| 4,319
| 49,548
| 0,897
| 55,153
| 7,546
| 1,220
| 1,021
| 17,704
| 7,805
| | 3,20
| 3,974
| 49,548
| 1,557
| 55,903
| 7,777
| 1,805
| 0,580
| 18,118
| 6,941
| | 3,60
| 4,349
| 73,616
| 2,368
| 79,917
| 11,337
| 0,974
| 0,789
| 25,842
| 10,859
| | 4,00
| 3,793
| 110,245
| 1,709
| 116,098
| 15,584
| 1,663
| 0,740
| 39,463
| 14,285
| | 4,40
| 3,573
| 163,384
| 1,653
| 168,979
| 22,483
| 0,661
| 1,071
| 55,872
| 17,603
| | 4,40
| 3,039
| 164,015
| 2,560
| 169,288
| 22,550
| 0,798
| 1,100
| 57,341
| 17,465
| | 4,40
| 3,640
| 163,393
| 2,645
| 168,913
| 21,936
| 0,466
| 0,727
| 58,558
| 17,755
| | 4,80
| 4,317
| 244,048
| 2,929
| 249,964
| 31,013
| 0,958
| 0,677
| 86,558
| 25,328
| | 4,80
| 4,059
| 243,730
| 2,191
| 249,343
| 31,013
| 0,767
| 0,348
| 85,732
| 25,703
| | 5,20
| 2,696
| 363,135
| 2,461
| 368,943
| 43,775
| 1,257
| 0,579
| 125,656
| 34,399
| | 5,20
| 2,239
| 363,001
| 2,571
| 368,567
| 43,046
| 1,225
| 0,478
| 127,545
| 33,827
| | 5,20
| 2,357
| 363,629
| 2,397
| 369,236
| 43,038
| 0,357
| 0,746
| 127,110
| 35,363
| | 5,60
| 3,584
| 541,317
| 2,682
| 547,496
| 60,534
| 0,202
| 0,592
| 188,287
| 49,029
| | 6,00
| 2,008
| 807,743
| 2,754
| 813,163
| 83,958
| 0,907
| 0,725
| 282,008
| 68,467
| Подгруппа 1
| X
| З н а ч е н и я ф у н к ц и и g (x)
| | Вар.10
| Вар.11
| Вар.12
| Вар.13
| Вар.14
| Вар.15
| Вар.16
| Вар.17
|
| | -6,00
| 17,092
| 43,273
| 24,173
| 13,494
| 4,244
| 0,888
| 200,677
| 37,842
|
| | -5,40
| 12,289
| 32,262
| 16,501
| 10,691
| 4,268
| 0,459
| 148,878
| 26,494
|
| | -5,40
| 13,638
| 32,594
| 16,630
| 11,143
| 4,259
| 0,880
| 148,641
| 26,931
|
| | -5,30
| 12,574
| 31,211
| 18,471
| 10,618
| 4,318
| 1,287
| 141,324
| 25,526
|
| | -5,20
| 12,288
| 29,390
| 17,800
| 10,171
| 4,253
| 1,094
| 134,487
| 24,203
|
| | -4,90
| 9,291
| 26,738
| 13,231
| 9,188
| 4,344
| 1,325
| 115,706
| 19,846
|
| | -4,90
| 10,210
| 24,883
| 13,711
| 9,522
| 4,267
| 1,110
| 115,775
| 20,568
|
| | -4,60
| 8,644
| 22,764
| 12,889
| 8,583
| 4,314
| 1,038
| 99,563
| 16,862
|
| | -4,50
| 6,870
| 23,113
| 12,846
| 8,140
| 4,294
| 1,432
| 94,907
| 15,996
|
| | -4,50
| 6,696
| 20,728
| 13,570
| 8,192
| 4,278
| 1,400
| 94,769
| 16,481
|
| | -4,00
| 5,971
| 18,630
| 9,605
| 7,157
| 4,378
| 2,005
| 73,619
| 11,979
|
| | -3,50
| 3,838
| 13,122
| 8,593
| 6,597
| 4,407
| 2,719
| 57,396
| 8,932
|
| | -3,30
| 3,549
| 14,262
| 8,402
| 6,294
| 4,402
| 2,615
| 51,951
| 8,829
|
| | -3,30
| 2,780
| 13,008
| 8,993
| 5,933
| 4,405
| 3,022
| 51,787
| 8,010
|
| | -2,60
| 0,788
| 9,312
| 6,819
| 5,287
| 4,579
| 4,435
| 36,644
| 6,156
|
| | -2,60
| 2,368
| 10,907
| 8,061
| 5,319
| 4,546
| 4,710
| 36,680
| 5,724
|
| | -2,40
| 0,949
| 10,998
| 5,611
| 5,292
| 4,586
| 4,883
| 33,393
| 5,460
|
| | -2,00
| 0,599
| 7,837
| 6,680
| 5,057
| 4,691
| 6,659
| 27,313
| 4,528
|
| | -2,00
| 0,611
| 7,895
| 6,751
| 5,011
| 4,781
| 6,712
| 27,253
| 4,863
|
| | -2,00
| 0,584
| 7,652
| 6,523
| 5,214
| 4,569
| 6,458
| 26,536
| 4,211
|
|
Продолжение аблицы 1.1
Подгруппа 2
| X
| З н а ч е н и я ф у н к ц и и g (x)
| | Вар.1
| Вар.2
| Вар.3
| Вар.4
| Вар.5
| Вар.6
| Вар.7
| Вар.8
| Вар.9
| | 2,00
| 1,377
| 1,173
| 10,498
| 4,306
| 5,806
| 2,119
| 0,930
| 14,382
| 7,156
| | 2,00
| 1,314
| 1,269
| 1,701
| 4,383
| 6,077
| 2,168
| 0,969
| 11,205
| 7,195
| | 2,00
| 1,486
| 1,080
| 3,066
| 2,984
| 5,797
| 2,033
| 1,001
| 14,495
| 7,879
| | 2,30
| 1,101
| 0,952
| 16,665
| 4,070
| 6,740
| 1,923
| 0,862
| 7,222
| 7,642
| | 2,70
| 0,567
| 0,722
| 21,145
| 3,170
| 6,828
| 1,810
| 0,520
| 18,392
| 8,878
| | 2,70
| 0,784
| 0,643
| 8,949
| 3,335
| 7,060
| 1,749
| 0,635
| 25,037
| 8,849
| | 3,20
| 0,520
| 0,270
| 38,887
| 4,409
| 7,107
| 1,426
| 0,389
| 34,943
| 9,130
| | 3,20
| 0,406
| 0,460
| 40,434
| 5,008
| 7,852
| 1,511
| 0,463
| 44,313
| 9,817
| | 3,60
| 0,340
| 0,146
| 53,240
| 4,984
| 8,256
| 1,551
| 0,303
| 42,676
| 9,800
| | 3,80
| 0,165
| 0,096
| 50,310
| 4,134
| 9,010
| 1,412
| 0,219
| 68,621
| 11,023
| | 4,00
| 0,320
| 0,085
| 72,313
| 4,545
| 8,537
| 0,969
| 0,231
| 76,762
| 10,732
| | 4,00
| 0,158
| 0,195
| 59,621
| 5,601
| 8,548
| 1,200
| 0,339
| 78,802
| 11,382
| | 4,00
| 0,324
| 0,223
| 50,076
| 4,759
| 9,267
| 1,338
| 0,184
| 69,960
| 11,525
| | 4,10
| 0,238
| 0,228
| 75,654
| 6,197
| 8,675
| 1,049
| 0,224
| 75,959
| 11,820
| | 4,10
| 0,299
| 0,257
| 64,703
| 6,177
| 8,834
| 1,244
| 0,173
| 80,592
| 11,762
| | 4,60
| 0,134
| 0,054
| 109,233
| 5,533
| 9,837
| 0,860
| 0,243
| 127,799
| 12,954
| | 4,60
| 0,176
| 0,152
| 101,045
| 6,528
| 9,553
| 0,968
| 0,117
| 135,033
| 12,695
| | 4,60
| 0,127
| 0,138
| 88,895
| 4,827
| 10,470
| 1,010
| 0,184
| 117,709
| 12,905
| | 4,80
| 0,056
| 0,103
| 100,339
| 6,672
| 10,679
| 0,805
| 0,105
| 157,594
| 12,909
| | 5,00
| 0,016
| 0,204
| 141,672
| 7,180
| 10,802
| 0,661
| 0,029
| 183,355
| 13,141
| Подгруппа 2
| X
| З н а ч е н и я ф у н к ц и и g (x)
| | Вар.10
| Вар.11
| Вар.12
| Вар.13
| Вар.14
| Вар.15
| Вар.16
| Вар.17
|
| | -2,00
| 4,274
| 2,647
| 6,397
| 3,670
| 3,122
| 1,102
| 1,231
| 1,791
|
| | -2,00
| 3,894
| 3,172
| 5,911
| 3,436
| 2,741
| 1,589
| 0,855
| 1,946
|
| | -1,50
| 3,068
| 3,579
| 5,524
| 3,402
| 2,619
| 1,502
| 1,727
| 2,115
|
| | -1,00
| 4,897
| 4,208
| 4,762
| 3,094
| 2,545
| 1,819
| 1,447
| 2,400
|
| | -1,00
| 4,848
| 3,643
| 5,318
| 3,421
| 2,433
| 1,726
| 1,601
| 2,360
|
| | -0,50
| 4,098
| 4,356
| 4,388
| 3,125
| 1,980
| 1,751
| 1,582
| 2,557
|
| | -0,50
| 4,853
| 3,031
| 4,716
| 3,101
| 1,986
| 1,830
| 2,164
| 2,452
|
| | 0,00
| 4,909
| 4,509
| 3,972
| 3,038
| 2,023
| 1,907
| 2,062
| 3,302
|
| | 0,00
| 5,414
| 3,794
| 3,966
| 3,168
| 2,122
| 1,793
| 2,245
| 3,429
|
| | 0,80
| 5,859
| 4,590
| 3,706
| 2,790
| 1,599
| 2,589
| 2,893
| 3,441
|
| | 0,80
| 5,571
| 4,160
| 3,029
| 2,908
| 1,561
| 2,428
| 2,625
| 3,646
|
| | 0,80
| 5,306
| 4,744
| 3,333
| 3,019
| 1,608
| 2,557
| 2,856
| 4,257
|
| | 1,20
| 6,822
| 4,691
| 3,465
| 2,801
| 1,783
| 2,311
| 3,079
| 4,290
|
| | 1,60
| 6,871
| 4,777
| 3,286
| 2,333
| 1,254
| 2,885
| 3,363
| 4,821
|
| | 1,60
| 5,891
| 6,037
| 2,516
| 2,417
| 1,299
| 2,915
| 3,544
| 4,726
|
| | 2,10
| 7,134
| 5,682
| 2,360
| 2,500
| 1,265
| 2,837
| 3,867
| 5,308
|
| | 2,70
| 8,305
| 7,148
| 2,078
| 2,456
| 1,228
| 3,221
| 4,994
| 6,678
|
| | 2,70
| 8,406
| 6,270
| 2,121
| 2,064
| 1,281
| 3,549
| 4,591
| 6,956
|
| | 2,70
| 9,421
| 6,901
| 2,406
| 2,051
| 1,327
| 3,380
| 4,615
| 6,321
|
| | 3,00
| 8,712
| 6,779
| 2,633
| 1,997
| 1,053
| 3,571
| 5,415
| 7,453
|
|
Таблица 1.2
Аналитический вид функции F (g (x), x) и пределы интегрирования
| Подгруппа 1
|
| Подгруппа 2
| | №
вар
| F (g (x), x)
| Пределы интегрирования
|
| №
вар
| F (g (x), x)
| Пределы интегрирования
| | a
| b
|
| a
| b
| |
| 
| 1,0
| 7,0
|
|
| 
| 1,0
| 6,0
| |
| 
| -1,0
| 5,0
|
|
| 
| 0,5
| 6,5
| |
| 
| -6,0
| 0,5
|
|
| 
| 1,0
| 8,0
| |
| 
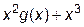
| -4,0
| 3,0
|
|
| 
|
| 8,0
| |
| 
| 0,5
| 6,5
|
|
| 
| 1,0
| 7,0
| |
| 
| 2,0
| 7,0
|
|
| 
| 0,5
| 5,5
| |
| 
| 1,0
| 7,0
|
|
| 
|
| 8,0
| |
| 
| -2,0
| 2,0
|
|
| 
|
| 6,0
| |
| 
| 1,0
| 3,0
|
|
| 
| 1,0
| 6,0
| |
| 
| -3,0
| 2,0
|
|
| 
| -3,0
| 3,0
| |
| 
| -1,0
| 1,0
|
|
| 
| -4,0
| 4,0
| |
| 
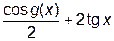
| -4,0
| -2,0
|
|
| 
| -2,0
| 4,0
| |
| 
| 0,5
| 5,0
|
|
| 
| -4,0
| 2,0
| |
| 
| 1,1
| 6,0
|
|
| 
| -5,0
|
| |
| 
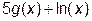
| 0,1
| 5,0
|
|
| 
| -5,0
| 5,0
| |
| 
| 0,1
| 5,5
|
|
| 
| -4,0
| 4,0
| |
| 
| -1,0
| 3,0
|
|
| 
| -2.0
|
|
Таблица 2
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...
Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...
Почему важны муниципальные выборы? Туристическая фирма оставляет за собой право, в случае причин непреодолимого характера, вносить некоторые изменения в программу тура без уменьшения общего объема и качества услуг, в том числе предоставлять замену отеля на равнозначный...
|
Задержки и неисправности пистолета Макарова 1.Что может произойти при стрельбе из пистолета, если загрязнятся пазы на рамке...
Вопрос. Отличие деятельности человека от поведения животных главные отличия деятельности человека от активности животных сводятся к следующему: 1...
Расчет концентрации титрованных растворов с помощью поправочного коэффициента При выполнении серийных анализов ГОСТ или ведомственная инструкция обычно предусматривают применение раствора заданной концентрации или заданного титра...
|
|
