Методом простых итераций определить корень уравнения
где
ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ ЗАДАЧИ 2 1) Решить на интервале [ xn, xk ] с разбиением его на 20 частей обыкновенное дифференциальное уравнение (3) первого порядка y′;= f (x, y) при начальных условиях y (x0)= y0 методом Эйлера и методом Рунге-Кутта 4-го порядка. 2) Построить диаграмму с графиками найденных решений (тип графика для метода Эйлера – отдельные точки, для метода Рунге-Кутта – гладкая кривая). 3) С помощью интерполяционного полинома Ньютона аппроксимировать функцию y (x) полиномом третьей степени P3 (x) в окрестности точки пересечения y (x0) с осью абсцисс, для чего: - из таблицы значений y (x0), найденной по методу Рунге-Кутта 4-го порядка, выбрать четыре последовательные точки, ближайшие к оси абсцисс и расположенные по обе стороны от нее; - по выбранным четырем узловым точкам построить интерполяционный полином Ньютона P3 (x); - подстановкой в полином P3 (x) значений абсцисс узловых точек проверить правильность найденных его коэффициентов на выполнение условий Лагранжа. 4) Методом простых итераций c точностью Найденный корень уравнения P3 (x)= 0 рассматривать как приближенное решение уравнения (2) и в целом задачи 2.
Дифференциальное уравнение, начальные условия и промежуток интегрирования уравнения выбираются из таблицы 2 по номеру подгруппы и номеру студента в журнале подгруппы. СОДЕРЖАНИЕ ОТЧЕТА ПО КУРСОВОЙ РАБОТЕ В отчет по курсовой работе необходимо включить следующие разделы:
|

 ,
,
 - решение задачи Коши
- решение задачи Коши ,
, 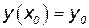 .
.
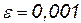 найти корень уравнения P3 (x)= 0. Для использования метода простых итераций преобразовать уравнение P3 (x)= 0 к виду x=P3 (x)+ x и найти значение коэффициента С, обеспечивающее сходимость метода.
найти корень уравнения P3 (x)= 0. Для использования метода простых итераций преобразовать уравнение P3 (x)= 0 к виду x=P3 (x)+ x и найти значение коэффициента С, обеспечивающее сходимость метода.


