Этапы построения прогноза по временным рядам
Прогнозирование экономических процессов, которые могут быть представлены одномерными временными рядами, сводится к выполнению следующих этапов: 1. Предварительный анализ данных; 2. Построение модели, т.е. выбор кривых, описывающих явление, и численное оценивание параметров модели; 3. Проверка адекватности моделей и оценка их точности; 4. Выбор лучшей модели; 5. Расчёт точечного и интервального прогноза. Охарактеризуем некоторые из этих этапов. При предварительном анализе данных происходит выявление аномальных отклонений, проверка наличия тренда, сглаживание временных рядов и расчёт показателей развития динамики экономических процессов. Выявление аномальных отклонений производится с помощью критерия Ирвина: Пусть y1, y2,..., yn – временной ряд. Вычислим значение критерия
S – несмещённое среднеквадратическое отклонение данного ряда
Далее проверяется гипотеза
Выявление тренда обычно происходит визуальным образом и зависит от опытности исследователей. Основная цель – угадать функцию, по которой развивается процесс. Здесь требуется информация о самом явлении. При построении модели используется понятие кривых роста. Обычно используют кривые роста, стараясь выбрать кривую максимально простого вида:
Подборка коэффициентов и выбор моделей осуществляется на основании метода МНК (метод наименьших квадратов). Пусть Оценка качества построенной модели Пусть построена некоторая модель, на основании которой вычислено значение
Для того, чтобы модель могла считаться хорошей, необходимо доказать, что ряд остатков
1. Проверка равенства нулю математического ожидания. Выдвигается основная гипотеза
Для проверки этой гипотезы строится критерий или случайная величина Стьюдента:
Здесь
2. Проверка условия случайности возникновения отдельных отклонений от тренда. Например, метод поворотной точки: точка
3. Проверка наличия или отсутствия автокорреляции в отклонении модели. Автокорреляция означает, что некоторое значение
Для статистики Дарбина-Уотсона также существуют таблицы критических значений. В этих таблицах указывается интервал 4. Соответствие ряда остатков нормальному закону распределения. Используется RS-критерий:
Если значения RS согласно таблице критерия попадает между критическими значениями Модель считается адекватной, если выполняются все пункты.
|

 , где
, где  .
. – выборочное среднее ряда или средний уровень ряда.
– выборочное среднее ряда или средний уровень ряда. : «аномальные данные отсутствуют». По таблицам для критерия Ирвина находится
: «аномальные данные отсутствуют». По таблицам для критерия Ирвина находится  , если
, если  , то yt считается нормальным; если
, то yt считается нормальным; если  , то yt считается аномальным. В этом случае аномальное значение исключается из ряда данных и вместо него подставляют обычно среднеарифметическое из двух соседних значений.
, то yt считается аномальным. В этом случае аномальное значение исключается из ряда данных и вместо него подставляют обычно среднеарифметическое из двух соседних значений. – линейный тренд;
– линейный тренд; – квадратичный тренд;
– квадратичный тренд; – экспоненциальный тренд.
– экспоненциальный тренд. – прогнозное (вычисление по модели) значение.
– прогнозное (вычисление по модели) значение.  – наблюдавшийся уровень ряда. Коэффициенты модели подбираются таким образом, чтобы сумма
– наблюдавшийся уровень ряда. Коэффициенты модели подбираются таким образом, чтобы сумма  . Модель, для которой достигнут такой минимум, считается наилучшей. Например, при
. Модель, для которой достигнут такой минимум, считается наилучшей. Например, при  (уравнение регрессии).
(уравнение регрессии). – значение, вычисленное по модели;
– значение, вычисленное по модели; – остаток в определении
– остаток в определении  является случайным и подчиняется нормальному закону распределений. Для доказательства используются:
является случайным и подчиняется нормальному закону распределений. Для доказательства используются: , то есть проверяется
, то есть проверяется 

 – несмещённое среднеквадратичное отклонение ряда остатков. По таблице распределения Стьюдента при
– несмещённое среднеквадратичное отклонение ряда остатков. По таблице распределения Стьюдента при  (заданном) находим
(заданном) находим 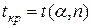 Если
Если  – считают, что
– считают, что  – считают, что
– считают, что  . Вероятность
. Вероятность 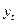 считается поворотной, если она одновременно меньше или больше двух соседних значений. Считается, что остатки случайны, если поворот точки приходится на каждые 1,5 значения. Если больше или меньше, то остатки нельзя считать случайными и модель следует уточнить.
считается поворотной, если она одновременно меньше или больше двух соседних значений. Считается, что остатки случайны, если поворот точки приходится на каждые 1,5 значения. Если больше или меньше, то остатки нельзя считать случайными и модель следует уточнить.
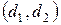 , при попадании в который, принимается то или иное решение. В частности, если
, при попадании в который, принимается то или иное решение. В частности, если  , то ряд остатков не коррелирован, если
, то ряд остатков не коррелирован, если  , то имеется корреляция. При
, то имеется корреляция. При  имеется неопределённость, и сделать вывод о наличии или отсутствии корреляции нельзя. В случае, когда
имеется неопределённость, и сделать вывод о наличии или отсутствии корреляции нельзя. В случае, когда  , говорят о наличии отрицательной автокорреляции. Если не удалось решить вопрос о наличии или отсутствии автокорреляции, то необходимо использовать более точные методы.
, говорят о наличии отрицательной автокорреляции. Если не удалось решить вопрос о наличии или отсутствии автокорреляции, то необходимо использовать более точные методы. , где
, где  – несмещённое среднеквадратичное отклонение.
– несмещённое среднеквадратичное отклонение. , то гипотезу о нормальном распределении принимают, в противном случае ряд из остатков нельзя считать нормально распределённым, а модель – хорошей.
, то гипотезу о нормальном распределении принимают, в противном случае ряд из остатков нельзя считать нормально распределённым, а модель – хорошей.


