Обоснование применения модели AR
Для того, чтобы обосновать применение модели авторегрессии, обычно рассматривается соотношение между двумя дисперсиями. Рассмотрим выражение (2) в случае
Рассмотрим Так как уровень ряда
Получаем, что Рассмотрим
Пусть по результатам наблюдений получены выборочные коэффициенты
Примеры анализа моделей: 1. Модель AR(1). Вид Система уравнений Юла-Уокера Оценка качества. Соотношение: Например, пусть 2. Модель AR(2). Вид Система Юла Уокера принимает вид:
Оценка качества. Подставим оценки коэффициентов в выражение для дисперсии:
Автокорреляционная функция – это коэффициенты автокорреляции
2 4
Для каждого процесса характерно своё поведение автокорреляционной функции.
Модели скользящего среднего MA(m ) Эти модели строят на основании предположения о том, что текущее значение уровня ряда представляется в виде линейной комбинации текущей и прошлых значений ошибки, то есть
где Напомним, Автокорреляционная функция имеет вид: Найдём коэффициенты автокорреляции для модели MA(m)
Вспомогательный результат
Рассмотрим его выражение при
Пусть теперь
Полученное выражение используется при идентификации моделей. Автокорреляционная функция модели MA(m)) обрывается после момента
MA(1) MA(2)
1 2 3 1 2 3
Получим выражение для коэффициентов автокорреляции. Для этого разделим Аналогично решению системы Юла-Уокера, для получения оценок коэффициентов модели M А необходимо вычислить выборочные коэффициенты автокорреляции Примеры нахождения оценок MA(1). Вид Выражение для дисперсии Пусть получено значение выборочного коэффициента автокорреляции, тогда получаем
Отсюда следует, что из двух корней полученного уравнения, один из корней всегда Вывод: модели скользящего среднего порядка 1 могут применяться только для описания процесса с автокорреляционной функции, обрывающейся после первой задержки и таких, что Оценим дисперсию для процесса MA(1), получаем:
Обобщение модели ARMA(p,q) или ARIMA(p,d,q) – модели авторегрессии скользящего среднего ARMA(p,q)=ARIMA(p,0,q). Эти модели основаны на предположении о том, что текущий уровень ряда Общий вид модели:
|

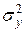 – дисперсия исходного процесса;
– дисперсия исходного процесса;  – дисперсия ошибки.
– дисперсия ошибки.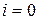 .
. .
.
 и текущий уровень ошибки
и текущий уровень ошибки  являются независимыми случайными величинами, то
являются независимыми случайными величинами, то  . Поэтому,
. Поэтому,
 .
.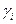 . Было введено, что коэффициент автокорреляции
. Было введено, что коэффициент автокорреляции 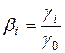 =>
=> 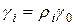 . Подставим полученное выражение в
. Подставим полученное выражение в  :
: 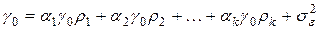 ,
,
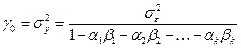 – выражение дисперсии ряда через дисперсию ошибки.
– выражение дисперсии ряда через дисперсию ошибки. , Тогда можно оценить отношение
, Тогда можно оценить отношение  . Модель считается хорошей, если
. Модель считается хорошей, если 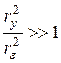 (гораздо больше).
(гораздо больше).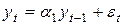 .
.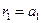 .
. . Видно, что чем ближе коэффициент
. Видно, что чем ближе коэффициент  к 1, тем выше качество модели
к 1, тем выше качество модели  .
.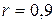 , тогда
, тогда  . При таком значении коэффициента корреляции дисперсия ошибки в 5 раз меньше дисперсии уровня ряда.
. При таком значении коэффициента корреляции дисперсия ошибки в 5 раз меньше дисперсии уровня ряда.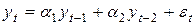 .
.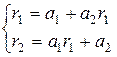

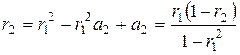 . Решение данной системы имеет вид:
. Решение данной системы имеет вид:  .
.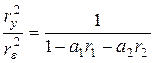 . После решения системы можно определить для полученной модели соотношение между дисперсиями. Анализ показывает, что при значении
. После решения системы можно определить для полученной модели соотношение между дисперсиями. Анализ показывает, что при значении 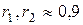 соотношение между дисперсиями также равно
соотношение между дисперсиями также равно  . Для модели AR(1), AR(2) можно наблюдать соотношение между дисперсиями
. Для модели AR(1), AR(2) можно наблюдать соотношение между дисперсиями  . Графическое изображение этих коэффициентов носит название корреллограмма. С её помощью идентифицируют модели авторегрессии скользящего среднего.
. Графическое изображение этих коэффициентов носит название корреллограмма. С её помощью идентифицируют модели авторегрессии скользящего среднего.












 1 3
1 3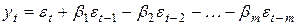 ,
, – параметры модели,
– параметры модели,  – порядок модели.
– порядок модели.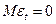 ,
, 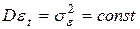 ,
, 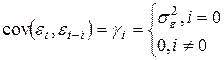 .
.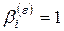
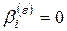
 .
. .
.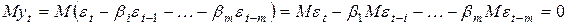 ,
,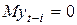 .
.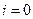 ,
,
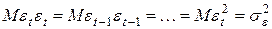 ,
,  .
. , тогда
, тогда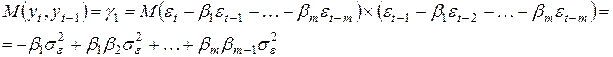 . Аналогично для любого
. Аналогично для любого  .
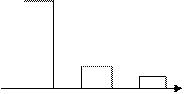
. :
:


 на
на  :
: 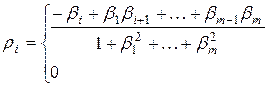 .
.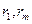 , подставить полученные выражения и получить оценки
, подставить полученные выражения и получить оценки 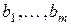 . Однако такую систему нужно решать численными методами.
. Однако такую систему нужно решать численными методами.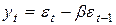 .
.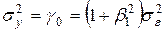 ,
, 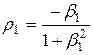 .
.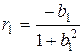 ,
,  ,
, 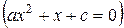 ,
,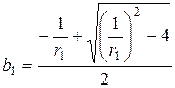 ,
, 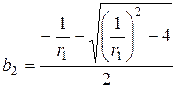 .
. 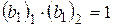 ,
, 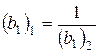 .
.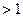 , а другой
, а другой 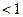 . Согласно теории стационарных процессов необходимым условием стационарности является
. Согласно теории стационарных процессов необходимым условием стационарности является  . Также необходимо, чтобы
. Также необходимо, чтобы 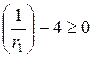 ,
, 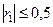 .
.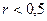 .
.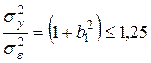 . Это означает, что точность модели MA равна 1,25 и относительный выигрыш в точности составляет менее 25%.
. Это означает, что точность модели MA равна 1,25 и относительный выигрыш в точности составляет менее 25%.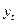 является линейной комбинацией p своих предыдущих уровней и q своих предыдущих ошибок. При идентификации модели ARMA(p,q) пользуются тем, что их автокорреляционные функции затухают плавно по экспоненте или синусоиде.
является линейной комбинацией p своих предыдущих уровней и q своих предыдущих ошибок. При идентификации модели ARMA(p,q) пользуются тем, что их автокорреляционные функции затухают плавно по экспоненте или синусоиде. .
.


