Некоторые определения из теории случайных процессов
Перейдём к изучению случайной составляющей временного ряда и построению математических моделей этой составляющей. Введём основные определения. Определение. Случайным процессом называется функция двух переменных Пусть зафиксирован элементарный исход эксперимента
t t1 t2 t3 t4
Определение.Временным рядом называется последовательность значений случайного процесса, взятых в некоторый момент времени То есть временной ряд можно рассматривать как последовательность случайных величин. Определение.Последовательность случайных величин называется стационарной, если
i j i+k j+k
Выражение (*) означает, что величины на любых двух непересекающихся промежутках времени одинаковой длины одинаково коррелированны. Определение.Ковариацией случайных величин Определение. Коэффициентом корреляции случайных величин Основные свойства коэффициента корреляции. 1. 2. Если случайные величины 3. Если величины Определение. Коэффициентом автокорреляции называется величина Здесь вводится понятие порядка автокорреляции. Например, коэффициент автокорреляции первого порядка имеет вид Коэффициент Определение. Последовательность случайных величин Таким образом, «белый шум» – это последовательность некоррелированных случайных величин, одинаково распределённых и имеющих нулевое математическое ожидание и постоянную дисперсию
Основным предположением построения модели является то, что текущее значение определяется некоторой предысторией и случайной ошибкой. В основном строятся модели не более чем второго порядка.
Рассмотрим пример вычисления коэффициента корреляции между случайными величинами Пусть даны случайные величины
Требуется рассчитать коэффициент корреляции и ответить, являются ли данные величины зависимыми? 1 этап. Восстановим частные распределения
2. Определим числовые характеристики величин x и y:
3. Вычислим совместное математическое ожидание этих случайных величин x и y:
4. Вычисление коэффициента ковариации:
Напомним, что коэффициент корреляции Так как в данном случае
|

 , где
, где  – элементарный исход эксперимента,
– элементарный исход эксперимента,  – время. Таким образом
– время. Таким образом  - функция двух переменных, принимающая вещественное значение.
- функция двух переменных, принимающая вещественное значение.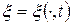 . Тогда эта функция выражает развития случайного явления во времени. Рассмотрим
. Тогда эта функция выражает развития случайного явления во времени. Рассмотрим





 t
t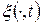 называется траекторией процесса, а набор значений
называется траекторией процесса, а набор значений  ,
,  ,... называется рядом.
,... называется рядом. ,
,  ,...,
,...,  .
.
 и
и  (*)
(*)  .
.
 и
и 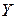 называется число
называется число  .
. .
. , т.е. коэффициент корреляции принимает значения от -1 до 1.
, т.е. коэффициент корреляции принимает значения от -1 до 1. (обратное неверно!)
(обратное неверно!) и наоборот.
и наоборот. , то есть коэффициент корреляции между уровнями временного ряда
, то есть коэффициент корреляции между уровнями временного ряда  и
и  .
. . Говорят, что это коэффициент с лагом 1.
. Говорят, что это коэффициент с лагом 1. – коэффициент автокорреляции с лагом
– коэффициент автокорреляции с лагом  .
. называется белым шумом, если
называется белым шумом, если  ,
,  ,
,  и
и 
 .
. . Иногда добавляется следующее требование:
. Иногда добавляется следующее требование:  которое означает, что величины
которое означает, что величины  . В этом случае говорят, что шум – гауссовский «белый шум».
. В этом случае говорят, что шум – гауссовский «белый шум».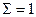
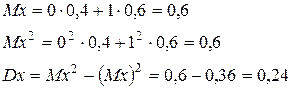


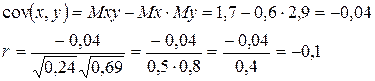
 .
. близко к нулю, величины
близко к нулю, величины 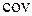 отрицательный, то величины
отрицательный, то величины 


