1. Взятие конечных разностей. Пусть исходный ряд  не является стационарным. Построим ряд
не является стационарным. Построим ряд  , где
, где  . Если этот ряд удовлетворяет условиям стационарности, то исходный ряд обозначают
. Если этот ряд удовлетворяет условиям стационарности, то исходный ряд обозначают  , и делают вывод, что исходный закон
, и делают вывод, что исходный закон  близок к линейному. В противном случае переходят к ряду
близок к линейному. В противном случае переходят к ряду  , где
, где  .Аналогично, обозначают
.Аналогично, обозначают  , и делают вывод, что закон
, и делают вывод, что закон  близок к квадратичному.
близок к квадратичному.
2. Логарифмирование цепных индексов, то есть  . Имеет место, если временной ряд
. Имеет место, если временной ряд  близок к экспоненте
близок к экспоненте  .
.
Процедуру интеграции приходится применять довольно часто, но после этого в стационарном ряде можно говорить о постоянстве коэффициентов автокорреляции второго порядка. В зависимости от характера поведения этих коэффициентов разделяют следующие процессы:
AR(k) –(autoregressive model)- модель авторегрессии порядка k; MA(m) – Moving Average – скользящее среднее порядка m; ARMA(k,m) – модель авторегрессии-скользящего среднего порядка k; ARIMA(k,d,m) – интегрированная модель авторегрессии-скользящего среднего, k-порядок авторегрессии, m- порядок скользящего среднего, d-порядок интеграции.
Перейдем к рассмотрению основных моделей.
Модель авторегрессии порядка k - AR(k)
Пусть имеется временной ряд  , или
, или 
 , где
, где  – текущее значение уровня.
– текущее значение уровня.
Основное предположение состоит в том, что текущее значение уравнения ряда  является линейной комбинацией k предыдущих значений и случайной ошибки.
является линейной комбинацией k предыдущих значений и случайной ошибки.
Общая модель авторегрессии:
 ,
,
где 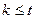 и
и  – параметры модели или коэффициенты модели,
– параметры модели или коэффициенты модели,  – случайная ошибка или «белый шум». При построении модели AR необходимо решить две задачи: какой порядок модели следует выбрать и чему равны коэффициенты модели. Решение этих вопросов называется процедурой оценки моделей.
– случайная ошибка или «белый шум». При построении модели AR необходимо решить две задачи: какой порядок модели следует выбрать и чему равны коэффициенты модели. Решение этих вопросов называется процедурой оценки моделей.
 (1).
(1).
Без ограничений предполагаем, что  .
.
{ Действительно, предположим  , тогда
, тогда  ,
, 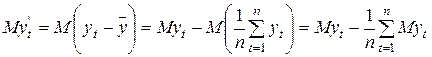 ,
,  ,
,  ,
,  . }
. }
Умножим выражение (1) на величину  и возьмём от полученного выражения математическое ожидание
и возьмём от полученного выражения математическое ожидание
 (2)
(2)
Рассмотрим выражение ковариации  . Введём обозначение
. Введём обозначение  - коэффициент автоковариации. Тогда выражение (2) может быть записано в следующем виде:
- коэффициент автоковариации. Тогда выражение (2) может быть записано в следующем виде:
 (2’)
(2’)
 .
.
Независимость следует из того, что ошибка текущего время не зависит от того, какие значения были получены до текущего момента времени  . Разделим уравнение 2’ на
. Разделим уравнение 2’ на 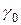 , получим
, получим
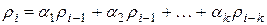 , (3)
, (3)
где  .
.
 – теоретический коэффициент автокорреляции порядка
– теоретический коэффициент автокорреляции порядка 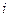 .
.
Таким образом, получили выражение для коэффициентов автокорреляции.
Нахождение коэффициентов модели. Для модели AR(k) имеет место (3). При помощи этого уравнения можно получить оценки коэффициентов 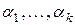 . Используется следующая идея: по результатам наблюдения
. Используется следующая идея: по результатам наблюдения  получим выборочные коэффициенты корреляции
получим выборочные коэффициенты корреляции 
 . Затем вместо теоретических коэффициентов автокорреляции подставляют в (3) выборочные значения и получают
. Затем вместо теоретических коэффициентов автокорреляции подставляют в (3) выборочные значения и получают
систему уравнений Юла-Уокера для определения оценок коэффициентов модели:
 (4)
(4)
 - оценки коэффициентов
- оценки коэффициентов 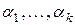
В этой системе известны  , неизвестны
, неизвестны  . Заметим, что с теоретической точки зрения оценки Юла-Уокера должны быть состоятельными и несмещёнными(см. курс теории вероятностей и математической статистики). Однако на практике это не всегда выполняется, наиболее сильно нарушается требование несмещённости. Причина заключается в том, что ошибки
. Заметим, что с теоретической точки зрения оценки Юла-Уокера должны быть состоятельными и несмещёнными(см. курс теории вероятностей и математической статистики). Однако на практике это не всегда выполняется, наиболее сильно нарушается требование несмещённости. Причина заключается в том, что ошибки  в действительности зависят от предыдущих значений
в действительности зависят от предыдущих значений  , но так слабо, что их полагают белым шумом. Однако это все-таки отражается на модели и снижает ее точность. Наиболее точно оценки коэффициентов модели можно получить для AR(1), AR(2)
, но так слабо, что их полагают белым шумом. Однако это все-таки отражается на модели и снижает ее точность. Наиболее точно оценки коэффициентов модели можно получить для AR(1), AR(2)

 не является стационарным. Построим ряд
не является стационарным. Построим ряд  , где
, где  . Если этот ряд удовлетворяет условиям стационарности, то исходный ряд обозначают
. Если этот ряд удовлетворяет условиям стационарности, то исходный ряд обозначают  , и делают вывод, что исходный закон
, и делают вывод, что исходный закон  близок к линейному. В противном случае переходят к ряду
близок к линейному. В противном случае переходят к ряду  , где
, где  .Аналогично, обозначают
.Аналогично, обозначают  , и делают вывод, что закон
, и делают вывод, что закон  . Имеет место, если временной ряд
. Имеет место, если временной ряд  .
. , где
, где  ,
,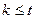 и
и  – параметры модели или коэффициенты модели,
– параметры модели или коэффициенты модели,  – случайная ошибка или «белый шум». При построении модели AR необходимо решить две задачи: какой порядок модели следует выбрать и чему равны коэффициенты модели. Решение этих вопросов называется процедурой оценки моделей.
– случайная ошибка или «белый шум». При построении модели AR необходимо решить две задачи: какой порядок модели следует выбрать и чему равны коэффициенты модели. Решение этих вопросов называется процедурой оценки моделей. .
. , тогда
, тогда  ,
, 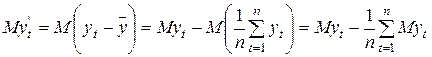 ,
,  ,
,  ,
,  . }
. } и возьмём от полученного выражения математическое ожидание
и возьмём от полученного выражения математическое ожидание (2)
(2) . Введём обозначение
. Введём обозначение  - коэффициент автоковариации. Тогда выражение (2) может быть записано в следующем виде:
- коэффициент автоковариации. Тогда выражение (2) может быть записано в следующем виде: (2’)
(2’) .
. . Разделим уравнение 2’ на
. Разделим уравнение 2’ на  , получим
, получим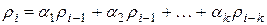 , (3)
, (3) .
. – теоретический коэффициент автокорреляции порядка
– теоретический коэффициент автокорреляции порядка 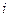 .
.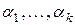 . Используется следующая идея: по результатам наблюдения
. Используется следующая идея: по результатам наблюдения  получим выборочные коэффициенты корреляции
получим выборочные коэффициенты корреляции 
 . Затем вместо теоретических коэффициентов автокорреляции подставляют в (3) выборочные значения и получают
. Затем вместо теоретических коэффициентов автокорреляции подставляют в (3) выборочные значения и получают (4)
(4) - оценки коэффициентов
- оценки коэффициентов  , неизвестны
, неизвестны  . Заметим, что с теоретической точки зрения оценки Юла-Уокера должны быть состоятельными и несмещёнными(см. курс теории вероятностей и математической статистики). Однако на практике это не всегда выполняется, наиболее сильно нарушается требование несмещённости. Причина заключается в том, что ошибки
. Заметим, что с теоретической точки зрения оценки Юла-Уокера должны быть состоятельными и несмещёнными(см. курс теории вероятностей и математической статистики). Однако на практике это не всегда выполняется, наиболее сильно нарушается требование несмещённости. Причина заключается в том, что ошибки  , но так слабо, что их полагают белым шумом. Однако это все-таки отражается на модели и снижает ее точность. Наиболее точно оценки коэффициентов модели можно получить для AR(1), AR(2)
, но так слабо, что их полагают белым шумом. Однако это все-таки отражается на модели и снижает ее точность. Наиболее точно оценки коэффициентов модели можно получить для AR(1), AR(2)


